電子磁気円二色性に基づく磁性材料の定量分析 　─超高圧走査透過型電子顕微鏡JEM-1000K RSによるナノ分解能測定へ─

はじめに

　今日電子顕微鏡法は単に原子スケールでの拡大像を得るためだけで無く、何種類かの分光器を備えることによって化学組成や電子状態の情報まで得ることができるようになった。特に試料を通過した電子を分析する電子エネルギー損失分光法（EELS）は豊富な物性情報をもたらし、同様な情報を与える競合的な手法としての放射光実験と比べ、サブナノメートルスケール領域分析が可能なためにその重要性は増す一方である。
　近年偏光方向を自由に制御できる最新の高強度放射光源によって固体の磁気的な性質を探ることが可能となった[1]。中でも「X線磁気円二色性（XMCD）」の発見が重要である[2-4]。XMCDとは入射光子の円偏光軸に対する吸収断面積の磁化方向依存性に起源を持つ。このXMCDスペクトルの積分強度に総和則（sum rules）を適用することで、試料のスピンおよび軌道磁気角運動量を定量的にかつ元素選択的に決定することができる[5,6]。XMCDに対応して、X線の代わりに透過電子顕微鏡（TEM）中で磁性試料を通過した電子を使って等価な情報を得る技法が「電子磁気円二色性（EMCD）」である[7-9]。すなわち内殻準位励起EELS測定によって元素選択的な磁性情報が抽出される。
　EMCDの可能性が2003年に最初に示されて以来[7]、最近のEMCDに関する実験テクニックの進展に伴って空間分解能が向上し[10,11]、さらに理論的な理解が進むことによって[12-16]、スピン/軌道磁気角運動量の最初の定量的な測定が報告された[17-19]。XMCDに比べ、 TEMによるMCD測定の空間分解能は遙かに高い。しかし元来信号強度が非常に小さいためにナノメートル分解能かつ定量的EMCD測定は未だに達成されていない。なぜなら内殻準位の吸収端スペクトルに載っているEMCD信号強度はエネルギー損失の関数としてべき乗則に従って減衰し、更にブラッグ回折点から外れた回折面上の点で測定されるために一層信号強度が小さくなるからである。また装置不安定性や試料ドリフト、高エネルギー電子照射による照射損傷が懸念される。これらの理由のためにこれまでほとんどの実験では、二波[8,14,17,20,21]または三波ブラッグ条件[11,17,19,22]で信号強度を最適化した実験配置で行われてきた。このことは翻って単結晶試料を正確な方位に長時間安定に設定する必要があることを意味する。
　本稿ではEELSを備えた超高圧走査透過型電子顕微鏡（UHV-STEM）を利用することによる新たなEMCD測定法を紹介する。従来のように特定の幾何学的配置及び回折条件で信号/ノイズ比（SNR）を最適化するのでは無く、多数のスペクトルを素早く取得し、さらに新しい統計解析法を適用することによって上述の困難を克服し、ナノメートルオーダーの空間分解能での定量的EMCD測定を実現した[23]。ここでは微細な多結晶鉄試料を例に本手法の有効性を示す。

理論的バックグラウンドとシミュレーション

　本稿で提案するアプローチは、回折面上におけるEMCD信号強度分布の計算機シミュレーションから発案されたものである[12,15]。双極子近似の範囲内で非弾性散乱の遷移行列要素（混合動的構造因子：MDFF）は結晶異方性も含めて非磁性成分と磁性成分の一次結合に常に分解できる[15]。鉄のように立方晶構造をもつ物質では異方性の項を無視することができ、MDFFの関数形S （q, q' , E）は次のように簡略化される：



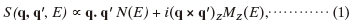
ここでq及びq' は運動量移送ベクトル、Eは損失エネルギー、N（E）及びM_Z（E）はそれぞれ非磁性スペクトル（たとえば遷移金属のL_2,3ホワイトライン）及びEMCD信号である。（1）式では測定試料は対物レンズの磁場によってz軸（TEM光軸）方向に磁化飽和していると仮定している。
　結晶軸、入射電子及び検出器の任意の相対的な方位関係に依存して散乱断面積（エネルギー損失スペクトル） ∂²(E,Ω)/∂E∂Ωはこれらの項の重み付き足しあわせによって次式のように表現される：



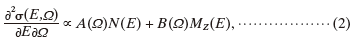
ただし重み関数A(Ω )及びB(Ω )は検出器の見込む回折立体角Ωの関数である。以上から十分に大きな結晶粒サイズを持つ立方晶試料からのEMCD信号は、未知係数A（Ω）及びB（Ω）によって非磁性信号N（E）とEMCD信号M_Z（E）が線形結合した形となっている。
　ランダム方位の多結晶試料に対する回折面上のEMCD信号分布のシミュレーション結果をFig.1に示す。体心立方晶の鉄単位胞4×4×18個（約1nm×1nm×5nm、576原子）からなるスーパーセルをMendelevらによって提案された原子間ポテンシャル[24]を用いる古典的分子動力学法によって溶融、徐冷した。この過程を何度も繰り返したところ数個の異なる方位を持つ結晶粒から成る多結晶構造モデルを得ることができた（Fig.1（a））。この構造から計算された電子回折図形をFig.1（b）に示す。このモデル構造に対して密度汎関数理論を適用し電子構造を計算した結果、一原子あたりの平均磁化が2.19μ_Bと見積もられた。更にこの構造に三次元周期境界条件を課して電子平面波入射による約600波を取り入れた動力学回折計算を行い[12,25]、最終的にFe-L₃ピーク位置で計算されたz軸方向の磁気信号成分の回折面上分布[16]をFig.1（c）に示す。このようにEMCD信号は、その強度と符号が様々に変化しながら回折面上のあらゆる点に分布している[12,15]。


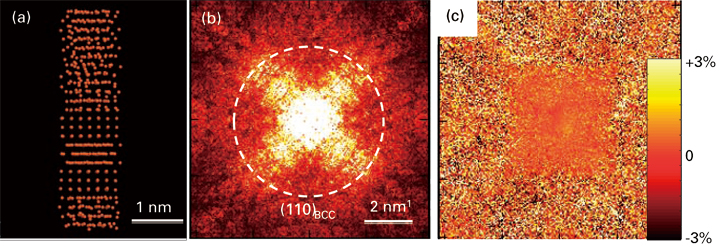
【Fig. 1　（a） 古典分子動力学によって生成した理論計算のための体心立方晶多結晶鉄のスーパーセル。（b） このスーパーセルで計算された電子回折図形（1 mrad ～ 0.25 g₁₁₀ ～ 1.25 nm⁻¹）。（c） z軸方向のEMCD信号強度（L₃ピーク強度に対する割合）の回折面上の分布。

実験方法

　厚さ50nmの非晶質Si₃N₄膜上に30nm厚の体心立方晶鉄膜と3nm厚のアルミキャップ層を超高真空チャンバー内で分子ビームエピタキシー法によって堆積させた。基板が非晶質であるため金属Fe/Al層は多結晶になっており、大気中でアルミキャップ層は酸化されて鉄多結晶膜の酸化保護膜の役割をはたす。Fig.2（a）に示すように結晶粒サイズはおよそ30nmで、膜厚と同程度であった。
　鉄薄膜の酸化によってFe-L₃及びL₂ピーク強度比が変化することが知られているため[26]、EMCD測定前後で試料膜の酸素のEELS元素分析を行った。酸化鉄と酸化アルミニウムの酸素スペクトルは容易に区別が付き、酸化鉄は検出限界以下（< 1at%）であった。
　EMCD測定は、名古屋大学の超高圧走査透過型電子顕微鏡（UHV-STEM）日本電子製 JEM-1000K RS（Fig.2（b））を用いて行った。加速電圧1MVで走査モードを用い、高加速電圧用に特別に設計されたガタンイメージフィルター（GIF）モデルQUANTUM相当品によってEELSスペクトルを記録した。測定中の集束電子ビームによって誘起される試料汚染対策のために試料をおよそ200℃に加熱し、さらにスペクトル強度をできるだけ稼ぐために電子ビーム電流を通常より増加させた。このためにゼロロスピーク（ZLP）の半値幅はおよそ2.6eVであった。
　実験配置の模式図をFig.3に示す。およそ5nm径の入射電子を試料上に集束させ、走査ステップ幅20nmで15×15標本点のデータを取得した。この条件下では、一標本点につき結晶粒一個～高々数個からスペクトルを取得することになる。入射電子の収束半角はおよそ1mrad、EELS検出器の分散設定は0.5eV/チャンネル、各点での露光時間30秒、検出器の取り込み半角約1mradという条件であった。検出器位置をFig.1（c）の中心から1.5 mrad離れた位置（透過波のすぐ近傍）に置いた条件で、様々な強度・符号の信号を収集することに対応する。測定中のFe-L₃ピーク強度はスペクトルあたり8,000-12,000カウントであった。


【Fig. 2　（a） 測定に用いた多結晶鉄膜のTEM像。（b）名古屋大学の超高圧走査透過型電子顕微鏡JEM-1000K RSの概観。】


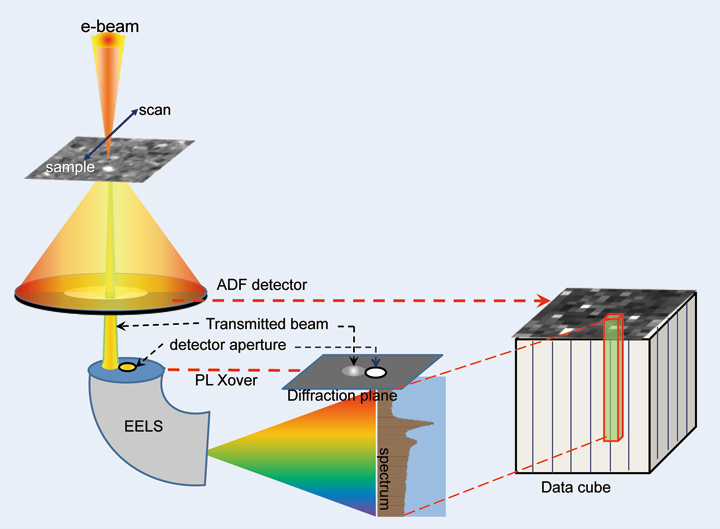
【Fig. 3　本実験セットアップと得られるデータ形式の模式図。（ADF: 環状暗視野、 PL: 投影レンズ）。 EELS検出器絞りはPLクロスオーバー位置に置かれる。】

結果

　上記の多数のスペクトルデータセットがEMCD信号を抽出するための統計処理への出発点となる。また超高圧電子顕微鏡の高加速電圧（1MV）を使用することでEMCD信号を歪ませる多重散乱効果[18,19,27]をかなりの程度まで抑制できる。我々の理論計算（Fig.4）及び検証実験[28]によると、試料厚さ25-40nmの範囲で正味のEMCD信号強度は200kVの場合に比べ約20%大きくなる。
　まずガタン社DigitalMicrograph™上の「SI/Align byPeak」及び「Volume/Remove x-rays」コマンドによってデータのピーク位置をそろえ、X線によるスパイクノイズを除去した。次にプリエッジバックグラウンドを減算してFe-L2,3ピークを抽出し、ローパスフィルター（窓幅3.5-10 eV）によってスペクトルのスムージングを行った。
　プラズモンピーク/ZLP強度比は6%以下で、多重ロスの最終的なm_L/m_S比評価への影響は実験精度に比べて無視しうる程度なので[18]、ここでは多重散乱効果を除去するための逆たたみ込み（deconvolution）処理をしていない。これも弾性/非弾性散乱平均自由行程の長い超高圧電子顕微鏡を用いることの利点である[28]。
　各スペクトルは740-750eVのポストエッジバックグラウンド領域が１になるように規格化される。この規格化が定量解析に及ぼす影響については既にこれまでの報告で議論した[29]。第一段階として、まず各データセットに属するスペクトルの全ての組み合わせ対に対して差スペクトルをとる。既に述べたように各スペクトルはEMCD信号と非磁性スペクトルの二つの成分から成り、ランダム方位で取得されたスペクトルでは各成分の重みもランダムに変化している。しかし一旦バックグラウンドが差し引かれてポストエッジ（この領域では磁性成分は常にゼロ）強度で規格化されていれば非磁性成分はすべてのスペクトルにおいて同じ強度になり、差スペクトルをとることによって除去される。
　さて各データセットに含まれる225本のスペクトルのすべての対の差スペクトルを計算するとデータセットあたり25,200本の差スペクトルが得られる。これらすべての差スペクトル一つ一つに対して、L₃及びL₂ピーク位置付近でのスペクトル強度の符号に次の（3）式のような判定基準を適用して有意なEMCD信号の存在の有無を判定する：



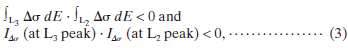
ただし、∫_L3 Δσ dEはL₃ピーク領域で積分したEMCD信号（差スペクトルΔσ）強度を、I Δσ（at L₃ peak）はL₃ピーク位置での差スペクトルの値を表す。（3）式の基準を満たした全ての差スペクトルに対してまずL₃ピーク位置での信号値を正に揃えて足し合わせる（Fig.7（a）参照）。実際には全差スペクトルの20-25%が（3）式の選択基準を満たした。これらの約5,000の差スペクトルには225本の元のスペクトルの内の100以上の独立したスペクトルが関与しており、したがって和スペクトルの統計ノイズは各スペクトルの平均ノイズに比べおよそ十分の一である。
　三つの異なる領域からそれぞれ取り出された信号和強度とそのプロファイルはFig.5（a）に示すようにほとんど同一のものとなった。相互のわずかな違いはプリエッジ及びポストエッジバックグラウンドの領域に見られ、これはノイズの多いプリエッジバックグラウンドをべき乗則でフィット、外挿することによって導入された誤差に起因する。これらの三つのEMCD信号を平均して得られた最終的なEMCDスペクトルをFig.5（b）に示す。EMCD信号強度はFe-L_2,3信号強度に対して2-2.3%程度と見積もられ、これは我々の理論的な見積もりとほぼ一致する（Fig.1（c）参照）。
　こうして得られたSNRの良いEMCD信号に次の（4）式で与えられるEMCD総和則[12]を適用し、軌道／スピン角運動量の比を評価する[13,14]：



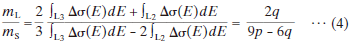
ただしq はEMCD信号Δσ（E）をL₃、L₂両ピーク領域にわたって積分した値、p はL₃エッジ領域のみにわたる積分値である。そこでFig.6（a）のようにp の値が１になるようにEMCDスペクトル全体を規格化すると磁気角運動量の比m_L/m_Sは一般性を失うこと無くq のみの関数となる。データスムージングに利用したローパスフィルターによってL₃及びL₂ピークのEMCD信号が重なり合い、互いに積算強度を打ち消しあうことがある。またさらにフィルターによってポストエッジ規格化に影響を与え [29]、総和則で決まるm_L/m_Sを変えてしまう。そこでFig.6（b）に示すように見積もられたm_L/m_S比を各ローパスフィルター窓幅の関数としてプロットした。q の値はポストエッジ領域（740-750 eV）からその最大・最小値を抜き出し、これによってm_L/m_S比の最大・最小値を求めた。この上限値と下限値をエラーバーとして中央値m_L/m_Sをプロットしている。各点の上限及び下限値の線形回帰線（灰色実線）による境界線で囲まれた領域に陰をつけた。m_L/m_S比の最終値は（中央値の線形回帰線の切片）±（各上下限値境界線の切片によって定義される間隔）÷2で与えられ、m_L/m_S = 0.0429 ± 0.0075と求められた。これは体心立方晶鉄に対するXMCDによって得られた値0.043[3]と良い一致を与え、多結晶膜に対して行われた最初の定量的EMCD測定となった。


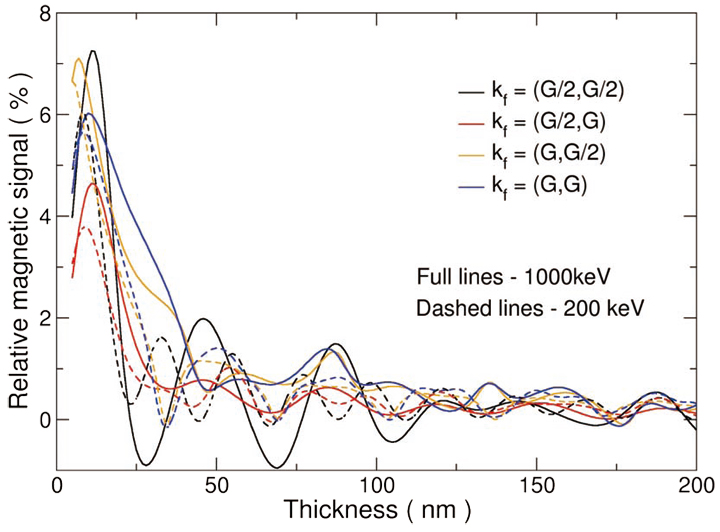
【Fig. 4　理論計算によるFe-L₃ピーク強度に対する正味のEMCD信号比（体心立方構造の鉄単結晶に<1‾1 8>入射、110系統反射励起条件）。各実線に対応する反射条件は凡例にGを単位（G = （110））としたLaue円中心位置で示されている。】


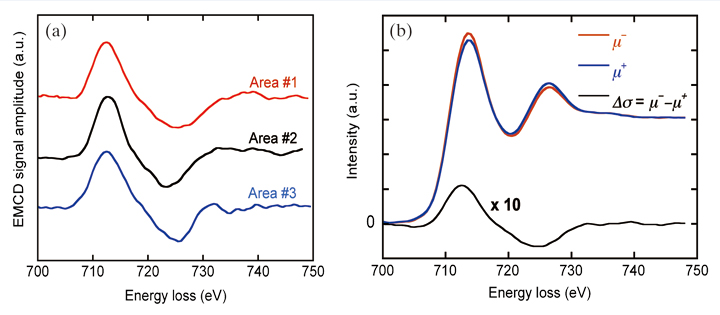
【Fig. 5　本研究で得られた代表的なEMCDスペクトル（窓幅5 eVのローパスフィルター適用） （a） 三つの異なる領域で別々に測定したデータからそれぞれ得られたEMCD信号。 （b） 最終的に得られた一対（μ⁺ and μ⁻）のFe-L_2、3 平均スペクトルとその差スペクトル（EMCD信号）Δσ= μ⁻−μ⁺。】


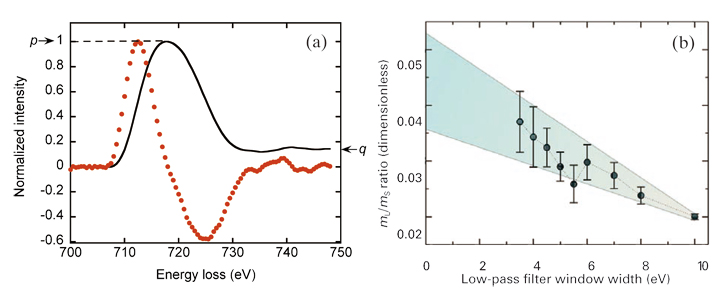
【Fig. 6　（a） 平均EMCD信号（赤線）及び総和則を適用するための積分（黒線）。（b）総和則から計算されたm_L /m_S比をローパスフィルター窓幅に対してプロット。】


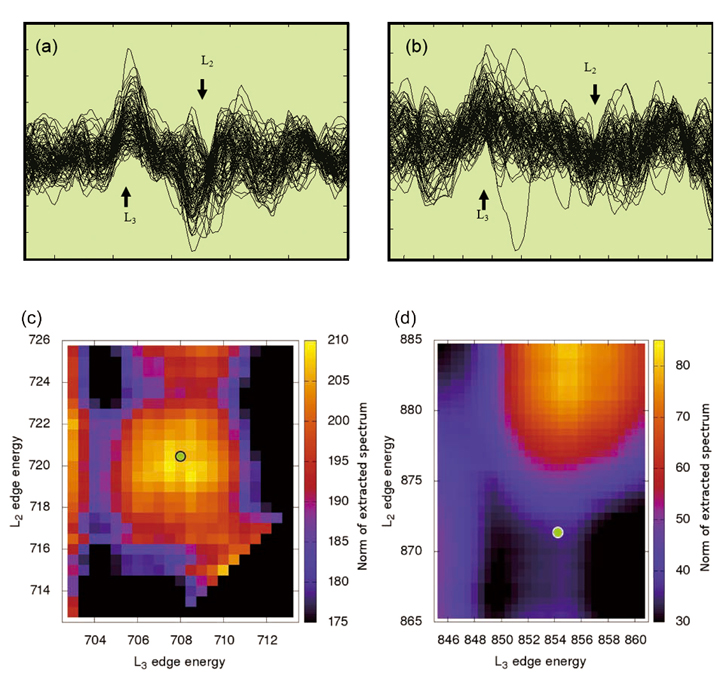
【Fig. 7　（a）体心立方晶多結晶鉄薄膜に対して得られた差スペクトルの例（（3）式の基準を満たし、符号を揃えて重ねたもの）。（b） 多結晶NiO膜に対して（a）と同じ処理をしたもの。矢印は元のL₃及びL₂ピーク位置を示す。（a）と（b）のデータの縦軸スケールの違いに注意（全てのスペクトルはポストエッジバックグラウンドで規格化されている）。（c） （3）式にしたがって鉄薄膜から平均EMCDスペクトルを取り出すために設定されたL₃及びL₂ピーク位置の関数としてのノルムマップ（考察参照）。（d） 反強磁性NiO膜に対する（c）と同じプロット。緑丸は正しいピーク位置を示す。ここでも強度スケールに注目されたい。】
 

考察

　EMCD信号の定量測定における主な問題点は、スペクトルドリフトやCCD検出器の残像効果などに起因する系統誤差である。そのために以前我々が提案した多変量スペクトル分解法[29]などのランダム誤差に基づく統計的信号抽出法が必ずしも効果的ではなく、今回のような選択基準（（3）式）に基づき有意な信号レベルを含んでいるデータをまず選別する必要があった。
　ランダムノイズを含むデータ列から偽のEMCD様信号プロファイルを取り出す可能性を排除するために、EMCD信号を示さない反強磁性NiO膜に対して同様の解析プロセスを適用した。試料として多結晶NiO薄膜（結晶粒径約30nm、膜厚約30nm）を、立方晶鉄膜と同様の実験条件（測定温度165℃（Néel温度以下））で測定し、同じデータ処理をNi-L_2,3スペクトルに対して適用した。
　生スペクトルとメディアンフィルター（各点の前後10チャンネルのデータ平均をとる）適用後のスペクトルとの差の二乗和をチャンネル数で割った値の平方根を取ることによってまずノイズレベルを見積もった。次にL₃ピーク位置でのEMCD平均信号強度をノイズレベルで割ることによってSNRを評価した。その結果多結晶鉄に対してSNRは2-3、一方NiOでは0.5以下であった。NiOデータから実際に取り出され平均化された信号はEMCD信号のような双こぶ形に見える。しかし総和則から計算されるq 値はときに物理的に意味の無い負の値をとるなど、フィルター窓幅に対して系統的な挙動を示さない。スペクトルが双こぶ形状をとるのは（3）式の選択基準によるもので、完全にランダムノイズスペクトルからでさえEMCD様の信号を取り出すことができる。しかし鉄多結晶膜から得られた信号プロファイルはFig.5（a）でみたようにきわめて安定な特徴を見せる。この状況は選択基準を満たした差スペクトルを重ねて示したFig.7（a）及び（b）によく反映されている：鉄多結晶膜では大まかなEMCD信号プロファイルが明らかに認められるが、NiO膜ではランダムノイズ振幅程度の傾向を示すのみである。
　NiO及び多結晶鉄から抽出したEMCD信号の統計的安定性の比較評価のために、 （3）式のL₃およびL₂ピークにおける積分範囲を変えながら平均EMCD信号を取り出し、それぞれのユークリッドノルム（各チャンネル値の二乗和）を設定したピーク位置の関数としてプロットする。もし真のEMCD信号が存在すればノルムは正しいピークエネルギー位置で局所極大を示すであろう。

　0.5eV間隔でピーク位置を順次変えて、そこからそれぞれ±5eVの範囲に（3）式の積分領域をとった場合のEMCD信号のユークリッドノルムのプロットをFig.7（c）及び（d）に示す。仮定したL₃ピーク位置を横軸に、L₂ピーク位置を縦軸にとり、緑丸が実際のL₃/L₂ピーク位置を表す。多結晶鉄膜のデータは実験ピーク位置から1eV以内の位置に極大を示すのに対し、NiOでは実験ピーク位置に目立った極大が見られないという明確な違いがあり、本解析法の有効性が示された。


 おわりに

　本稿ではエネルギー損失分光器を搭載した超高圧走査電子顕微鏡の利用によって、多結晶膜から統計的に有意なEMCDスペクトルが得られることを示した。今回5nm径のプローブを用いたが、全体として100nmオーダーの領域から抽出された結果であることを強調しておく。各データに十分な数のランダム方位結晶が含まれてさえいれば走査領域の大きさを小さくすることができる。したがって今回のアプローチは単結晶に限定せずナノスケールのいかなる試料に対しても定量的なEMCD測定を可能にし、ナノ磁性の分野においてEMCDの新たな応用可能性への道筋をつけたものである。
 

謝辞

　本研究を遂行するにあたり、名古屋大学の新超高圧電子顕微鏡の設置に携わっていただいた日本電子㈱の技術者諸氏、中でも大﨑光明、大田繁正両氏に心からの感謝を表したい。本研究の一部は日本学術振興会科学研究費補助金・新学術領域「ナノ構造情報のフロンティア開拓−材料科学の新展開」（「ナノ電子状態解析のフロンティア開拓」 25106004）及び若手研究Aの援助を受けた。

参考文献

[ 1 ] Stöhr, J. & Siegmann H. Ch. Magnetism: From fundamentals to Nanoscale Dynamics. Springer,ISBN 978-3-540-30283-4 （2006）.
[ 2 ] Erskine, J. L. & Stern, E. A., Phys. Rev . B 12, 5016-5024 （1975）.
[ 3 ] Schutz, G., Wagner, W., Wilhelm, W., Kienle, P.,Zeller, R., Frahm, R. & Materlik, G., Phys. Rev. Lett . 58, 737-740 （1987）.
[ 4 ] Chen, C. T., Idzerda, Y. U., Lin, H.-J., Smith, N.V., Meigs, G., Chaban, E., Ho, G. H., Pellegrin, E. & Sette, F., Phys. Rev. Lett . 75, 152-155 （1995）.
[ 5 ] Thole, B T., Carra, P., Sette, F. &. van der Laan, G., Phys. Rev. Lett. 68, 1943-1946 （1992）.
[ 6 ] Carra, P., Thole, B. T., Altarelli, M. & Wang,, Phys. Rev. Lett. 70, 694-697 （1993）.
[ 7 ] Hebert, C. & Schattschneider, P., 96, 463-468 （2003）.
[ 8 ] Schattschneider, P., Rubino, S., Hébert, C., Rusz,J., Kunes, J., Novák, P., Carlino, E., Fabrizioli, M.,Panaccione, G. & Rossi, G., Nature 441, 486-488 （2006）.
[ 9 ] Batson, P., Phys. Rev. Lett . 70, 1822-1825 （1993）.
[10] Schattschneider, P., Hébert, C., Rubino, S., Stoeger-Pollach, M., Rusz, J. & Novák, P., Ultramicroscopy 108, 433-438 （2008）.
[11] Schattschneider, P., Stoeger-Pollach, M., Rubino,S., Sperl, M., Hurm, Ch., Zweck, J. & Rusz, J., Phys. Rev. B 78, 104413 （2008）.
[12] Rusz, J., Rubino, S. & Schattschneider, P., Phys. Rev. B 75, 214425 （2007）.
[13] Rusz, J., Eriksson, O., Novák, P. & Oppeneer, P. M.,Phys. Rev. B 76, 060408（R） （2007）.
[14] Calmels, L. Houdellier, F., Warot-Fonrose, B.,Gatel, C., Hÿtch, M. J., Serin, V., Snoeck, E. &Schattschneider, P., Phys. Rev. B 76, 060409（R）（2007）.
[15] Rusz, J., Rubino, S., Eriksson, O., Oppeneer, P. M. &Leifer, K., Phys. Rev. B 84, 064444 （2011）.
[16] Rubino, S., Schattschneider, P., Rusz, J., Verbeeck,J. & Leifer, K., J. Physics D: Appl. Phys. 43, 474005（2010）.
[17] Lidbaum, H., Rusz, J., Liebig, A., Hjörvarsson, B.,Oppeneer, P. M., Coronel, E., Eriksson, O. & Leifer,K., Phys. Rev. Lett. 102, 037201 （2009）.
[18] J. Rusz, J., Lidbaum, H., Rubino, S., Hjörvarsson, B.,Oppeneer, P. M., Eriksson, O. & Leifer, K., Phys. Rev. B 83, 132402 （2011）.
[19] Warot-Fonrose, B., Gatel, C., Calmels, L., Serin, V. & Schattschneider, P., Ultramicroscopy 110, 1033（2010）.
[20] Warot-Fonrose, B., Houdellier, F., Hÿtch, M. J.,Calmels, L., Serin, V. & Snoeck, E., Ultramicroscopy 108, 393 （2008）.
[21] Zhang, Z. H., Wang, X. F., Xu, J. B., Muller, S.,Ronning, C. & Li, Q., Nature Nanotech . 4, 523（2009）.
[22] Stoeger-Pollach, M., Treiber, C. D., Resch, G. P.,Keays, D. A. & Ennen, I., Micron 42, 456-460 （2011）.
[23] Muto, S., Rusz, J., Tatsumi, K., Adam, R., Arai, S.,Kocevski, V., Oppeneer, P. M., Bürgler, D. E. & Schneider, C. M., Nature Commun . 5, 3138 （2014）: DOI: 10.1038/ncomms4138.
[24] Mendelev, M. I., Han, S., Srolovitz, D. J., Ackland, G.J., Sun, D. Y. & Asta, M., Phil. Mag. 83, 3977 （2003）.
[25] Rusz, J., Muto, S. & Tatsumi, K., Ultramicroscopy 125, 81 （2013）.
[26] Stöger-Pollach, M., Scripta Materialia , 69, 820-822 （2013）.
[27] Rusz, J., Novák, P., Rubino, S., Hébert, C. &Schattschneider, P., Acta Phys. Polonica A 113, 599（2008）.
[28] Tatsumi, K., Muto, S., Rusz, J., Kudo, T. & Arai, S.,Microscopy , in press （2014）: doi: 10.1093/jmicro/dfu002.
[29] Muto, S., Tatsumi, K. & Rusz, J., Ultramicroscopy 125, 89 （2013）.