モノクロメータ搭載STEM-EELSによる電子状態解析

はじめに

透過電子顕微鏡(TEM)に組み込まれる電子エネルギー損失分光法(EELS)のエネルギー分解能向上に関しては、これまで多くの研究開発がなされてきた。近年、新しい世代のモノクロメータが開発され、走査型透過電子顕微鏡(STEM)と併用することで、高エネルギー分解能で空間分解能の高い分析が可能になった。本稿では、京都大学化学研究所に設置されている、モノクロメータを搭載した(走査)透過電子顕微鏡の特性を簡単に紹介したあと、高分解能EELSを有効に活用した金属ナノ粒子に励起される局在表面プラズモンの研究と、内殻電子励起に現れる吸収端微細構造(ELNES)を有機結晶へ適用した例を紹介する。

モノクロメータ搭載 STEM-EELS (JEM-ARM200F)

モノクロメータを搭載した(走査)透過電子顕微鏡(日本電子製 JEM-ARM200F)の外観写真をFig. 1に示す。モノクロメータは、2段のウィーンフィルターと偏向コイルで構成されており、ショットキー型電子銃と加速管の間に組みこまれている[1]。1段目のフィルターの下部にはエネルギー分散したフォーカスビームが形成され、その位置にエネルギー選択スリットを挿入することで、電子の単色化が行われる。2段目のフィルターは、単色化されたビームをアクロマティックなビームに二次集束する役割を果たしている。そのため、電子源から放出された電子とモノクロメータ出口に集束された電子は1:1の関係になっている。ウィーンフィルターのエネルギー分散は12.3 μm/eVで、スリットの幅を変えることで電子のエネルギー幅を選択することができる。本装置では、スリット幅は0.1 μmから4 μmの間で7種類セットされており、スリット挿入時には、ゼロロスピークの半値幅から見積もられたエネルギー分解能を、30 meVから250 meVまで選択することができる。また、鏡体には照射系および結像系の球面収差補正装置(CEOS社製)が組み込まれており、高分解能STEM、TEM観察を可能にしている。分析装置は、イメージングフィルター Quantum ESR(Gatan社製)とエネルギー分散型X線分析装置JED-2300T SDD100GV(日本電子製)を装備している。また、加速電圧は200 kVと60 kVを選択することができ、低加速での測定も可能となっている。Fig. 2に200 kVの加速電圧で、0.1 μmのエネルギー選択スリットを挿入した場合のゼロロスピークを示す。比較のために、冷陰極電界放出電子銃(Cold-FEG)で測定されたスペクトルも表示している。ピークの半値幅は33 meVで、Cold-FEGと比較して一桁狭く、1 eV以下の近赤外領域のゼロロスピークの裾強度が大幅に低減している。このように、スペクトルの測定可能領域が低エネルギーに広がったため、以下で述べる表面プラズモンの研究に威力を発揮するだけでなく、振動励起の検出も可能になってきた[2、3]。

Fig. 1 モノクロメータを搭載したJEM-ARM200Fの外観写真

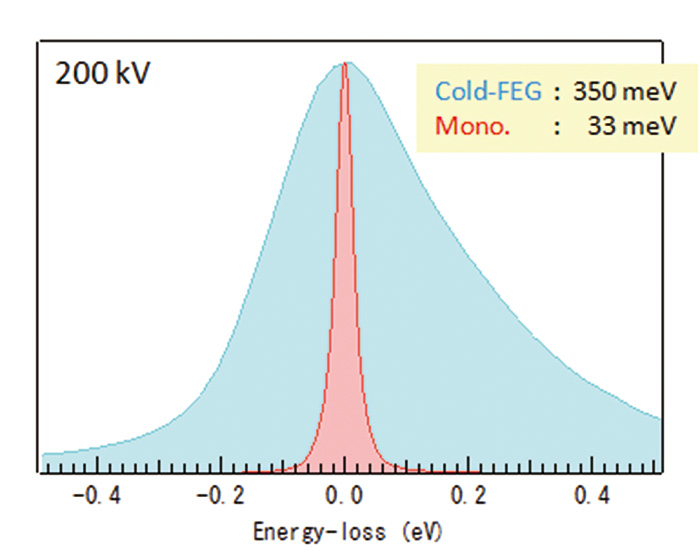
Fig. 2 モノクロメータ動作時のゼロロスピークとCold-FEGのゼロロスピーク

エネルギー選択スリットは0.1 μm。加速電圧はいずれも200 kV。

局在表面プラズモンに対する誘電体基板効果

金属ナノ粒子に光や電子を照射すると、局在表面プラズモン(LSP)と呼ばれる表面モードが励起される。これは、表面の価電子の集団振動によるもので、ナノ粒子近傍には強い近接場光を伴っている。LSPの共鳴条件は、粒子のサイズや周囲の環境に敏感なことから、バイオセンサーや光触媒への応用が研究されている。LSPの物理的な性質をより詳細に調べるためには、単一のナノ粒子に対して、高い空間分解能で分析する必要がある。走査型透過電子顕微鏡(STEM)と高エネルギー分解能EELSを組み合わせた手法は、近赤外領域のEELSをサブnmの空間分解能で効率よく計測できるため、LSPの研究には最適の方法であり、多くの研究が報告されている[4]。以下ではLSP励起に対する誘電体基板効果の研究について紹介する。
Fig. 3には、MgO基板上に支持された銀ナノ粒子に対して、高エネルギー分解能STEM-EELSによって測定された結果を示す[5]。この測定の特徴は、基板とナノ粒子の界面に平行に電子プローブを入射させているため、LSP励起に対する基板効果を、界面からの距離の関数として捉えることが可能な点にある。STEM-EELSによるスペクトラムイメージデータは、収束角24.6 mradの電子プローブを0.4 nmステップで走査させ、EELSの取り込み角度29.2 mrad、エネルギー分解能70 meVで取得した。HAADF像(a)から粒子は直径14 nmで、ほぼ球形であることがわかる。図に示した3つの場所(A、B、C)から抽出したスペクトルをFig. 3(b)に示す。入射プローブの位置によりLSP共鳴エネルギーは僅かに異なっており、粒子のトップの位置(A)の共鳴エネルギーは、横の位置(B)に比べて80 meV低エネルギーシフトしている。また、共鳴エネルギー付近3.40 ± 0.20 eVの強度を用いたEELSマップをFig. 3(c)に示す。MgO基板が存在することにより、球状の銀ナノ粒子に励起されるLSP励起確率分布は非対称で、界面から離れた粒子トップ位置の強度が強く、界面付近で弱い特徴的な分布を示している。このようなピークシフトや非対称な強度分布は、LSPに対する誘電体基板の効果と考えられる。これを理解するために、離散双極子近似(DDA)によるシミュレーションを行った。

Fig. 3 MgO基板上の銀ナノ粒子に励起された局在表面プラズモン

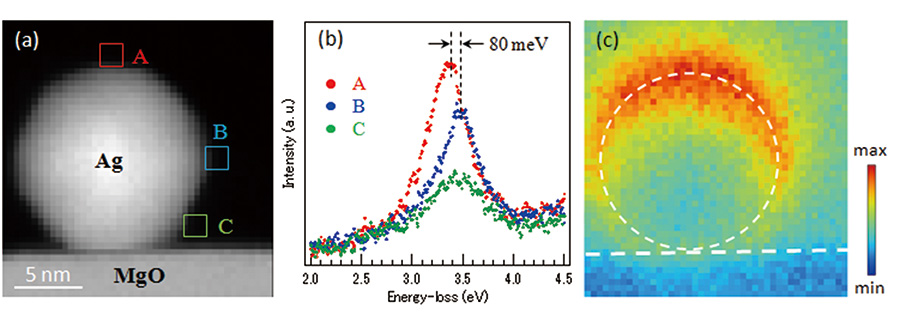
(a)HAADF像 (b)3つの異なる位置から得られたEELSスペクトル (c)LSP共鳴ピークの強度を用いたEELSマップ

MgO基板に支持された直径14 nmの銀ナノ粒子に対して、 DDEELSコード[6]を用いて計算したシミュレーション結果をFig. 4に示す。計算において、銀の誘電関数はPalikのデータ[7]を用い、MgOの誘電率は3.13[8]の一定値を仮定した。異なる位置に電子プローブが入射した場合について計算されたEELSスペクトルをFig. 4(a)に示す。LSP共鳴エネルギーやスペクトル強度の相対関係は、実験結果を良く再現している。図には3つの異なる入射位置におけるスペクトルに加え、比較のために基板が存在しない場合のスペクトルも示している。基板がない孤立ナノ粒子の場合のスペクトルに比べ、基板が存在する場合には、共鳴ピークが全体的に僅かに低エネルギーシフトしており、これは誘電率が大きい物質が粒子近傍に存在する時に生じる現象として知られている。一方、入射位置(A)および(B)における共鳴エネルギーの違いは、銀ナノ粒子に励起されたLSPの双極子モードの分極方向に関係している。すなわち、電子が(A)の位置に入射した場合、粒子に誘起される分極は基板との界面に対して垂直になるのに対し、(B)に入射した場合は、分極の方向は界面に対し平行になる。このような基板に対するLSPの分極の方向による共鳴エネルギーシフトは、直線偏向した光の実験においても観察されている[9]。EELSの場合、電子プローブの入射位置を選択することによって、光の偏向スペクトルと等価な結果が、高い空間分解能で得られることが明らかになった。また、入射位置(A)における共鳴ピークの強度は、基板がない場合に比べ増加しているのに対し、界面付近の(C)に入射した場合には、顕著な強度の減少がみられる。このようなLSP共鳴ピーク強度の空間分布は、Fig. 4(b)のEELSマップのシミュレーション結果においてより明瞭に示されており、Fig. 3(c)の実験結果と同様に、非対称な強度分布が得られている。基板効果によって、このような分布になる理由を理解するためには、EELS励起確率の計算法に立ち戻る必要がある。

Fig. 4 DDEELSによるシミュレーション

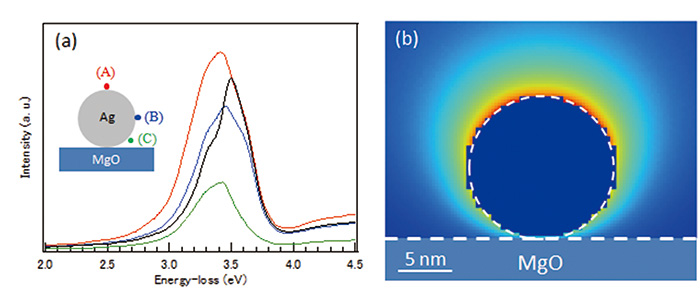
(a)3つの異なる位置における計算スペクトルと孤立した銀ナノ粒子近傍のスペクトル（黒線） (b) LSP共鳴励起によるEELSマップの計算結果

DDEELSコードでは、金属ナノ粒子を離散的な双極子の集合体と考える。EELSの励起確率は、位置r_jにある双極子のモーメントP_jと入射電子プローブによる印加電場E_j^appの積を、すべての双極子について和をとることによって計算される。双極子モーメントは、その点における局所電場に比例する。局所電場は電子プローブによる印加電場と他の双極子による電場の和であるため、EELSの励起確率は、入射電子プローブの位置に依存した印加電場の分布に強く依存することが予想される。基板に支持されたナノ粒子の場合、構造の対称性が低下するだけでなく、誘電体基板の分極によって印加電場の強度分布も変化する。誘電体基板の効果は、鏡像電荷モデルによって考慮することができる。すなわち、界面をx=0とした時、(x_e, y_e, z_e)に入射する電子によって分極する基板の電場は、(−x_e, y_e, z_e)に位置する鏡像電荷qによって求めることができる。
鏡像電荷は、基板のMgOの誘電率をε_MgOとした時、q=(1−ε_MgO) e/(1+ε_MgO)で表すことができる。ここで、eは電荷素量である。ε_MgOは1よりも大きな値であるため、qは正となる。したがって、基板による分極電場は、入射電子と鏡像電荷の間の領域では、入射電子による電場を増強させる作用を及ぼすことになる。Fig. 5には、基板効果を考慮した印加電場分布をDDEELS法によって計算した結果を示す。電子がナノ粒子のトップ領域に入射した場合（Fig. 5(a)）、印加電場はナノ粒子の広い部分に分布している。これは、粒子中の多くの双極子を励起することを意味しており、結果としてLSPの励起確率は高くなる。それに対して、電子プローブが界面付近に入射する場合(Fig. 5(c)）、入射電子の電場は基板内の鏡像電荷の電場によって打ち消され、ナノ粒子内に分布する印加電場は界面付近に限られた領域となっている。その結果、励起される双極子もFig. 5(a)の場合に比べて減少し、LSPの励起確率が低くなる。電子がナノ粒子の側面付近に入射する場合には(Fig. 5(b)）、粒子内に分布する印加電場の分布は、孤立した粒子の場合(Fig. 5(d))と類似の分布となっており、基板による影響が弱いことを示唆している。これは、基板効果が強く現れる入射電子と基板との間の電場分布が、ほとんど真空領域であるため、LSPの励起にほとんど関与しないためである。実際、Fig. 4(a)の計算スペクトルでは、ナノ粒子側面に入射した場合のスペクトル強度は、孤立した粒子のスペクトル強度とほとんど等しいことが示されている。
誘電体基板が存在することにより、単一銀ナノ粒子に励起されるLSPの双極子モードは、分極方向の違いにより二つのモードに分離し、その励起確率は分極方向が基板に対して垂直な場合に強くなることが明らかになった。二つのモードの共鳴エネルギーの違いは僅かであるため、高エネルギー分解能STEM-EELSによる測定が有効であったことがわかる。

Fig. 5 DDEELSによる基板効果を考慮した印加電場分布

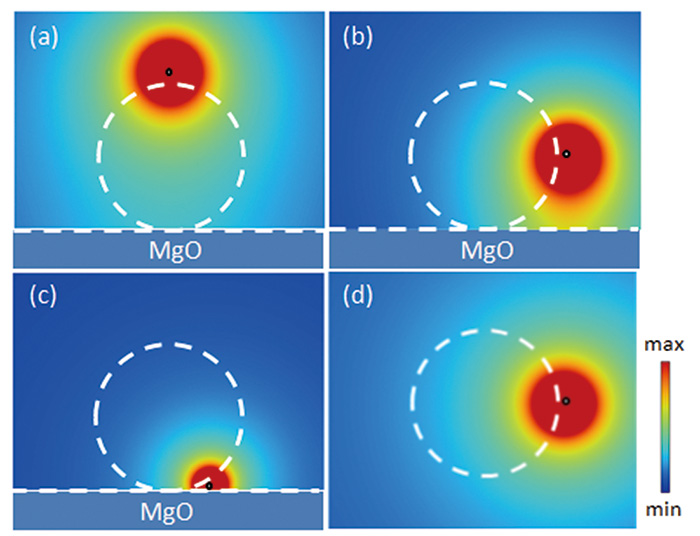
(a)から(c)は、MgO基板がある場合 (d)は孤立した銀ナノ粒子の場合

有機薄膜の高分解能EELS

内殻電子励起スペクトルに現れる吸収端微細構造(ELNES)の測定において、エネルギー分解能を制限する因子として、①入射電子のエネルギー幅、②エネルギー分析装置の分解能、③励起の始状態のエネルギー幅、④終状態の密度分布と寿命が挙げられる。モノクロメータと高分解能の分析装置を導入することにより、0.1 eV以下のエネルギー分解能でELNESを測定することは可能であるが、内殻励起に特有な③と④の因子によって、実際のELNESのエネルギー分解能は制限を受ける。
内殻電子が非占有電子バンドに遷移する際、内殻には空孔が生じる。その空孔の寿命は内殻準位のエネルギー幅を決定する。空孔の寿命は内殻空孔より浅い準位に存在する電子の崩壊に伴う特性X線やオージェ電子の生成に関連しており、内殻準位の束縛エネルギー (吸収端のエネルギー )に依存する。内殻準位のエネルギー幅は理論的に計算されており[10]、束縛エネルギーが大きな内殻準位ほど寿命は短くエネルギー幅は広くなり、スペクトルの高分解能測定が原理的に困難になることが知られている。一方、終状態のエネルギー幅は、励起電子が持つ運動エネルギー (損失エネルギーと内殻準位の束縛エネルギーの差)に依存する。励起電子が非弾性散乱される平均自由行程を用いた終状態のエネルギー幅の評価によれば、吸収端直上付近では終状態の寿命によるエネルギー幅は非常に小さいものの、吸収端から離れるにしたがい、終状態の寿命は短くなりスペクトルはブロードになると示唆されている[11]。したがって、遷移の寿命を考慮すると、高エネルギー分解能化の効果は、比較的浅い束縛準位から励起された吸収端直上付近のスペクトル構造に現れるといえる。さらに、ELNESは非占有バンドの部分状態密度分布(PDOS)を反映しているため、バンドの分散もスペクトルのブロードニングに関係する。実際、酸化物の酸素K殻ELNESの吸収端直上のピーク構造は、モノクロメータを用いた測定でも改善しないことが報告されており、その一因がバンド分散の効果にあると考えられている[12]。それに対して、以下で述べる有機薄膜結晶の場合、分子間の相互作用が弱く、バンド分散も小さいため、束縛エネルギーが小さい炭素のK殻ELNESの吸収端直上付近に現れるπ*ピークには、分子固有のスペクトル構造が現れると期待される。
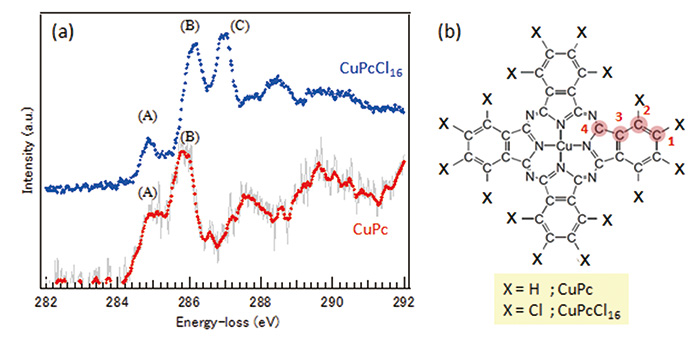
Fig. 6(a)には、銅フタロシアニン薄膜(CuPc)と塩素化銅フタロシアニン薄膜(CuPcCl₁₆)から測定された炭素K殻ELNESを示す[13]。CuPc分子はFig. 6(b)に示すように、環の中心に銅原子が配位した4回対称の平面分子である。分子周辺の水素原子を塩素に置き換えると、CuPcCl₁₆分子となる。CuPcCl₁₆分子は有機分子の中では電子線照射に対して最も強い分子の一つとして知られており、臨界電子線量は約30 C/cm²程度である。それに対しCuPc分子の臨界電子線量は1 C/cm²程度であるため、試料の電子線照射損傷に対する注意が特に必要である。Fig. 6(a)のスペクトルは、 STEM-EELSによる低ドーズ測定によって得られた。すなわち、入射プローブ電流をCuPc分子の場合0.05 pA、CuPcCl₁₆分子では1 pAとし、それぞれの試料の臨界電子線量以下でスペクトラムイメージデータを取得し、空間情報を平均化することでスペクトルのS/N比を向上させた。臨界電子線量が小さいため、CuPcから測定されたスペクトルのS/N比はあまり高くはないが、吸収端から4 eV付近までの微細構造において、CuPcCl₁₆のそれと明瞭な違いが観察されている。すなわち、ピーク(a)と(b)は両方の分子のスペクトルに現れているが、塩素化したCuPcCl₁₆のELNESでは、287 eV付近にCuPcとは異なるピーク(c)が現れている。これらのピークはすべて1s→π*遷移に帰属され、終状態は最低非占有分子軌道(LUMO)と考えられる。これらの分子内には、化学結合環境の異なる独立な炭素原子が3種類あり、Fig. 6(b)に示したように、周辺原子(水素もしくは塩素)および炭素と結合した原子(C1、C2）、すべて炭素と結合した原子(C3）、二つの窒素および炭素と結合した原子(C4)に分類される。これらの原子の1s準位の束縛エネルギーは僅かに異なることが、XPSの測定で知られており[14]、それがELNESのピークエネルギーの違いとして現れている。CuPc分子の場合、C1、 C2およびC3の1s準位はほとんど同じで、C4の束縛エネルギーが大きい。これは、C4サイトと結合している窒素の電気陰性度が大きいために、C4サイト上の価電子密度が他の炭素サイトに比べ低下し、価電子と1s電子とのクーロン反発エネルギーが減少したことに起因する。したがって、CuPcのスペクトルのピーク(a)はC1、C2、C3の励起、ピーク(b)はC4の励起と解釈することができる[15]。一方、 CuPcCl₁₆分子の場合は、C1、C2サイトに結合している塩素の電気陰性度が窒素よりも大きいため、C1、C2サイトの1s準位はC4よりも安定化し、その結果、ピーク(b)よりも高エネルギー側にC1、C2の励起ピークが現れる。したがって、CuPcCl₁₆のスペクトルのピーク(a)はC3の励起、ピーク(b)はC4の励起、ピーク(c)はC1、C2の励起と帰属することができる。各ピークの相対強度も含めた定量的な解釈を行うためには、内殻ホールの効果を考慮したスペクトル計算が必要となる。

Fig. 6 銅フタロシアニン薄膜の炭素K殻ELNESと分子構造モデル

この例で示されたように、有機結晶では分子間相互作用が弱いため、バンド分散が小さく、終状態は非占有分子軌道として近似できる。そのため、吸収端直上の微細構造には高エネルギー分解能化の効果が顕著に現れる。CuPcCl₁₆のピーク(b), (c)の間隔は0.7 eVと非常に狭いにもかかわらず明瞭に観察できており、内殻準位の化学シフトがELNESにおいても検出できることを示唆している。このような高分解能の炭素K殻ELNESの特徴を生かすことにより、有機分子に結合した官能基の識別による分子分析が可能になると期待される。
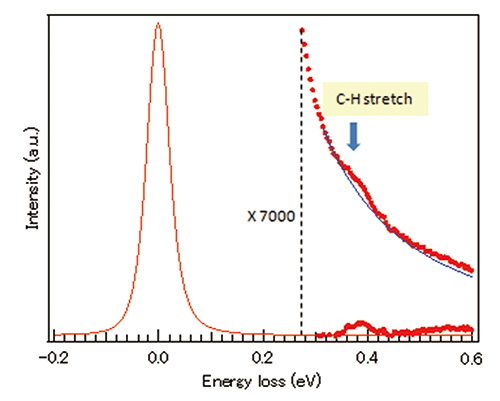
最後に、振動励起に関する結果を示す。有機分子の赤外吸収スペクトルには、様々な振動モードの励起が観察される。その多くは200 meV以下に現れるが、CuPc分子の場合、周辺のベンゼン環のC-H伸縮振動の励起が380 meV付近に現れることが知られている。 Fig. 7に示すように、高分解能EELSにより、C-H伸縮振動に帰属できるブロードなピークが観察された。しかし、その強度は弱く、h-BNなどで観察されている光学フォノン励起に比べてかなり弱い。このスペクトルは、照射電子線量が0.5 C/cm²で測定されており、臨界電子線量は下回っているものの、照射損傷の影響も無視することはできないと思われる。実際、臨界電子線量を僅かに上回る1.25 C/cm²で測定した場合には、このC-H伸縮振動の強度は消失しており、照射損傷の初期過程において、水素原子の解離が大きく寄与していると考えられる。このような、初期の損傷の影響は炭素K殻ELNESにおいても観察され、CuPc分子のELNESにおけるピーク(a)の強度が低下した。これは、水素原子の解離によるC1、C2サイトの結合状態の変化を示唆している。

Fig. 7 銅フタロシアニン薄膜から測定された振動スペクトル

おわりに

モノクロメータを搭載したSTEM-EELSは、可視から近赤外の低エネルギー損失領域に現れる表面プラズモン励起や振動励起を高い空間分解能で検出することを可能にした。また、高エネルギー損失領域に現れるELNESにおいては、有機結晶薄膜に対して低ドーズ量で測定することにより、炭素K殻の高エネルギー分解能ELNESが有益な情報を提供することを示した。今後、このような特徴を活かした分子分析の研究を展開する予定である。

謝辞

本研究の一部は科学研究費16K13625の助成を受けて行われました。

参考文献

• M. Mukai, E. Okunishi, M. Ashino, K. Omoto, T. Fukuda, A. Ikeda, K. Somehara, T. Kaneyama, T. Saitoh, T. Hirayama, Y. Ikuhara, Microscopy , 64, 151 (2015).
• T. Miyata, M. Fukuyama, A. Hibata, E. Okunishi, M. Mukai, T. Mizoguchi, Microscopy 63, 377 (2014).
• O. L. Krivanek, T. C. Lovejoy, N. Dellby, T. Aoki, R. W. Carpenter, P. Rez, E. Soignard, J. Zhu, P. E. Batson, M. J. Lagos, R. F. Egerton, P. A. Crozier, Nature, 514, 209 (2014).
• C. Colliex, M. Kociak, O. Stéphan, Ultramicroscopy 162, A1 (2016).
• Y. Fujiyoshi, T. Nemoto, H. Kurata, Ultramicroscopy 175, 116 (2017).
• N. Geuquet, L. Henrard, Ultramicroscopy 110, 1075 (2010).
• E. D. Palik, Handbook of Optical Constants of Solids 1, Academic Press, New York, (1985).
• E. D. Palik, Handbook of Optical Constants of Solids 2, Academic Press, New York, (1991).
• M. W. Knight, Y. Wu, J.B. Lassiter, P. Nordlander, N. J. Halas, Nano Lett . 9, 2188 (2009).
• M. O. Krause, J. H. Oliver, J. Phys. Chem. Ref. Data 8, 329 (1979).
• R. F. Egerton, Ultramicroscopy 107, 575 (2007).
• C. Mitterbauera, G. Kothleitnera, W. Groggera, H. Zandbergenb, B. Freitagc, P. Tiemeijerc, F. Hofer, Ultramicroscopy 96, 469 (2003).
• H. Kurata, Y. Fujiyoshi, Y. Tomisaki, T. Nemoto, M. Haruta, The 16th EMC Proc., Lyon, France, 863 (2016).
• F. Evangelista, V. Carravetta, G. Stefani, B. Jansik, M. Alagia, S. Stranges, A. Ruocco, J. Chem. Phys. 126, 124709 (2007).
• R. De Francesco, M. Stener, G. Fronzoni, J. Phys. Chem. A116, 2885 (2012).