キュリー・ワイスの法則とESR基本方程式に基づく定量分析法 "有効磁気モーメント法"
日本電子news Vol.49 No.3
松本 信洋
国立研究開発法人 産業技術総合研究所
物質の純度または濃度を物理量の測定値と物理定数等から直接求める事ができる定量分析法は、一次標準直接法と呼ばれており、分析化学・計量標準分野における基盤的な分析法である。しかしながら、この分析法の資格を潜在的に有している方法として国際的に認められているのは、重量分析法と電量分析法、凝固点降下法の3種類のみである。本研究は、キュリー・ワイスの法則と電子スピン共鳴(ESR)基本方程式を組み合わせることにより、第4の一次標準直接法の実現を目指している。「有効磁気モーメント」は不対電子による"ミニ磁石"の強さの事である。本定量分析法は、"閉殻電子"のみをもつ原子の中に一種類の不対電子をもつ原子が存在するとき、その不対電子をもつ原子の個数を直接測定することができる。本分析法のアプリケーションとしては、例えば、ESR定量分析の信頼性向上の効果があるスピン量標準試料が考えられる。
はじめに ~一次標準直接法について~
化学の一分野である分析化学は、試料中の目的元素あるいは化学種を識別する定性分析、その相対量あるいは絶対量を定める定量分析などの方法を探求する学問である[1]。その「分析化学」の教科書、例えば、赤石らの著書[1]では、最初に、酸-塩基の概念などの分析化学の基礎知識を学ぶ章の後で、古典的定量分析法(基準分析法)である重量分析法、容量分析法の章が配置されている。そして、その後の章で数多くの機器分析法が記述されている。ただし、機器分析法の一つである電量分析法も基準分析法として取り扱われている[2]。標準物質の生産方法について記述されている国際規格ISO Guide35:2006[3]の定義によれば、重量分析法と電量分析法は、「一次標準測定法」の一種である「一次標準直接法(primary direct method)」の資格を潜在的に有する分析法に属する。一次標準直接法は、同じ量の標準を参照することなく未知の値を測定可能であり、純度または濃度と国際単位系(SI)を直接結びつける事ができる定量分析法である。Table 1(a)に、一次標準直接法の特徴をまとめた。例えば,電量分析法の場合、周知の通り、金属イオンの物質量を電気量とファラデー定数、金属イオンの価数から求めることができる。国際度量衡委員会物質量諮問委員会(CCQM)で承認されているのは、この電量分析法と、重量法(重量分析法)と電量分析法の他、凝固点降下法の三種類のみである。容量分析法は、もう一種類の一次標準測定法である一次標準比率法(primary ratio method)に該当する。"同じ量の標準に対する未知のものの比の値を測定する"定量分析法であり、同位体希釈質量分析法もこれに該当する。定量NMR法[4]、中性子放射化分析法[5]も何らかの方法で純度または濃度が決定済みの標準物質を必要とする。
既存の一次標準直接法は、いずれもアボガトロ定数程度以上の "マクロ"な原子数をもつ試料に適用されるものであり、今日では良く確立されている信頼性のある科学法則に基づいている。それに対して筆者は、磁気工学・磁性学分野で良く確立されている「キュリーの法則」[6]に基づく定量分析法 "有効磁気モーメント法(effective magnetic moment method)"の開発に取り組んでいる[7-8]。その特徴をTable 1(b)に示した。固体物性学・固体化学研究では、例えば、純度を100%とみなした新規化合物の磁気感受率の温度依存性を測定して、その化合物を構成するイオンの価数を推定するために、キュリーの法則が用いられることがある。それに対して、本研究では、その逆を試みることによって定量分析法を試みるものである。
Table 1
| (a)国際度量衡局物質量諮問委員会で承認されている一次標準直接法[3-4] | (b)有効磁気モーメント法 | |||
| 重量法 | 電量分析法 | 凝固点降下法 | ||
| 学術分野 | 無機化学 | 電気化学 | 熱力学 | 固体物性学(磁性) |
| 科学法則 | - | ファラデーの法則 | Van't Hoff 方程式 | キュリー・ワイスの法則およびESR基本方程式 |
| 主な装置 | 天秤 | 滴定装置 | 断熱型熱量計 | 磁力計 電子スピン共鳴測定装置 |
| 分析対象成分の例 | 無機塩 | 金属イオン | 高純度有機液 | 希土類イオン、フリーラジカル、遷移金属イオン |
| 分析法の概要 | 溶液中での特定の沈殿量を測定 | 特定の物質を電気分解させたときの電気量を測定 | 融点付近における融解量と温度の関係を測定 | 電子の熱エネルギーが十分に大きい温度領域で磁気モーメントと温度の関係を測定 |
| 測定方程式 | ng = w Mw-1 a | nq = Q (zF)-1 b | xp = 1-ΔfusH ΔT (RT02)-1 c | n = 3kB cCurie (μ0μeff2 H)-1 d |
ang は物質量. w は質量. Mwはモル質量.
bnq は物質量. Qは電気量. z はイオンの価数. Fはファラデー定数.
cxp は純度. ΔfusH はモル融解エンタルビー.ΔT は融点降下. R は気体定数. T0 は純物質の融点.
dn, kB, cCurie, μ0 , μeff, H は本解説における原理のセクション参照
既存の一次標準直接法、および、本研究による"有効磁気モーメント法"の特徴。
「有効磁気モーメント法」の原理
「有効磁気モーメント法」が適用可能な試料のマトリックスは、閉 殻構造をもつ電子("閉殻電子")のみをもつ原子で構成されている必要がある。定量分析対象成分は量子フリースピン(不対電子)をもつ原子であり、その例として、希土類イオン、遷移金属イオン、有機フリーラジカルがある。「有効磁気モーメント」は不対電子の量子フリースピンによる"ミニ磁石"の大きさである。有効磁気モーメント法は、閉殻電子と不対電子が示す磁気感受率の温度依存性の違いを利用する。Fig. 1(a)に示されているように、質量Wの試料に印加する磁界の強さ(磁場)Hが一定のとき、閉殻電子による磁気モーメントは温度に依存しない一定の値を示す。それに対して、量子フリースピンによる磁気モーメントはキュリーの法則に従って温度Tに反比例する(ランジュバン常磁性)。ただし、キュリーの法則は電子間相互作用、および、結晶場などの周囲の原子からの影響が全くない前提で成立する。実際には、分子磁界による相互作用の強さを表す補正パラメーターであるワイス温度Θがキュリーの法則に導入された「キュリー・ワイスの法則」に従うことが多い。Fig. 1(b)のように、縦軸に試料の磁気モーメントm、横軸にΘで補正された温度の逆数をとったプロットを行うと、切片は閉殻電子による磁気モーメントの総和m0となる。それに対して、傾きcCurieは、試料中に存在する不対電子をもつ原子の個数nに比例した値となる。mは超伝導量子干渉計(SQUID)のような比較的感度の良い磁力計で測定する。
試料中の不対電子をもつ原子の個数nは以下の測定方程式によって求めることができる。
n = 3kB cCurie(μ0μeff2 H )‒1···········(1)
ここで、kB、μ0はボルツマン定数、真空の透磁率である。この式の導出は文献[8]に詳細に記載した。μeffは有効磁気モーメントの大きさであり、
μeff = gJ [J (J +1)]½μB ≡ pμB···········(2)
である。gJ はランデのg因子、Jは合成角運動量である。両方とも、パウリの排他原理とフントの規則に基づく電子配置から理論的に求める事ができる。μBはボーア磁子、pは有効磁子数である。cCurieは、SQUIDで測定するmとTのデータの組について以下の式にフィッティングさせることにより求める。
m = cCurie(T ‒ Θ)‒1 + m0···········(3)
Fig.1 本定量分析法の原理
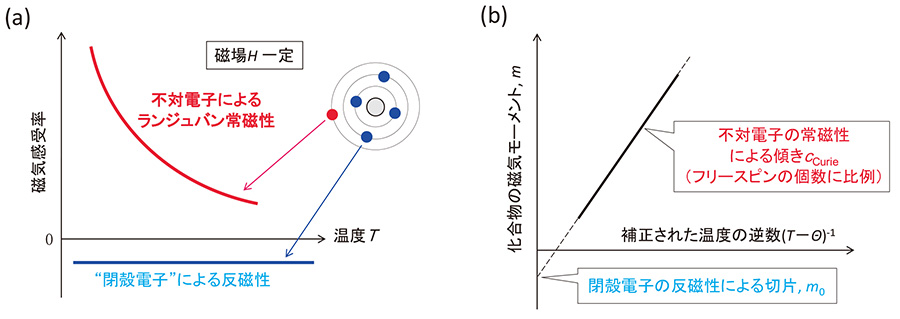
(a)不対電子と閉殻電子の磁気感受率の温度依存性の違い、(b)キュリー・ワイスの法則に基づくフリースピン定量の概念図。
原理の妥当性確認 ~希土類イオンの定量~
上記の原理に基づく主な実験手順をFig. 2のフローチャートに示した。この原理で実際に定量がどの程度可能なのかを確認するために、反磁性物質である酸化ケイ素(SiO2)粉末中に存在する酸化ガドリニウム(Gd2O3)の定量を試みることにした。Gd2O3を選択したのは、 化学的安定性の他に、希土類イオンの4f電子軌道が5s、5p、6s 軌道よりも内側にあるために4f電子が外からの相互作用を受けにくく、自由イオンであるとみなしやすい事、および、ガドリニウムイオン(Gd3+)の4f電子軌道に異方性がなく理想的な球状の電荷分布をしており、その事によって、原理の妥当性確認がしやすいのではないかと期待したためである。Gd3+の7個の4f電子はパウリの排他原理とフントの規則により、合成スピン角運動量S=7/2、合成軌道角運動量L=0をもつ。その結果、合成角運動量とランデのg因子はJ=S=7/2、gJ =2、となる。ゆえに、Gd3+のpの理論値は7.9373となる。
市販のGd2O3およびSiO2高純度粉末(メーカーによる差数法による純度は99.999%以上)を原料として質量比混合法で調製した複数の濃度が異なる混合物粉末試料を、本分析法の原理の妥当性を確認するための試料とした。各粉末の純度は1 kg/kgであり、両化合物とも化学量論的組成をもつとみなして、各粉末の秤量値からGd2O3の「調製濃度」xgravを求めた。そして、xgravと本分析法で得られる分析濃度xanalの比較を行った。
Fig.2
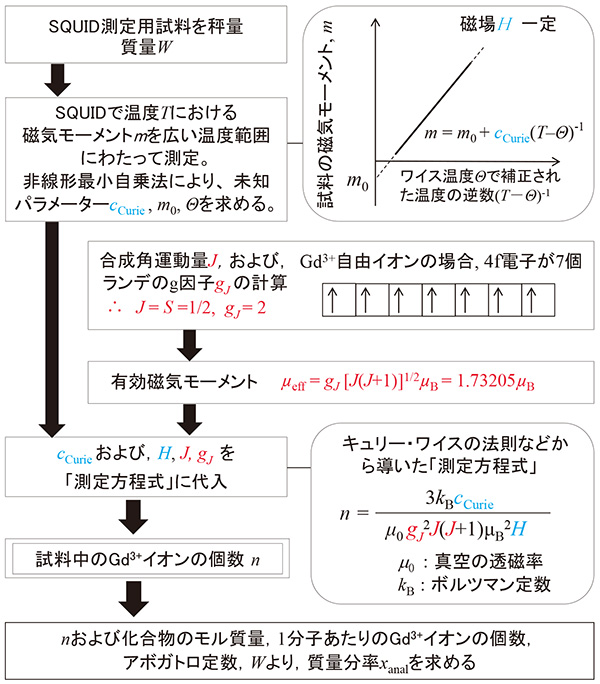
"有効磁気モーメント法"の妥当性確認を目的とした酸化ガドリニウム定量の場合の分析手順。
Fig. 3は磁気モーメントmを測定するSQUIDの構造を簡略化して示したものである。測定試料の大きさは長さ9 mm以下、直径6 mm以下という制限がある。粉末試料の場合は、ゼラチンなど反磁性の材料で作られているカプセルに封入する。そして、そのカプセルを中に入れたストロー(試料ホルダー)を試料上下移動用ロッドに取り付ける。試料空間内は大気圧未満のヘリウムガス雰囲気下にある。超電導磁石により発生している一定の磁場環境下で、測定試料を超伝導線検出コイルの中に入れると、検出コイル内の試料位置に依存した出力電圧が得られる。そして、磁気モーメント標準試料を測定した場合の出力電圧の試料位置依存性と比較することにより、磁気モーメント値が求まる。なお、試料空間における磁場、温度、検出される磁気モーメントについて、NMR磁場測定器、または、白金測温抵抗体、米国標準技術研究所の磁気モーメント標準物質を用いて校正することにより、SIへの計量計測トレーサビリティを確保した。
Fig.3
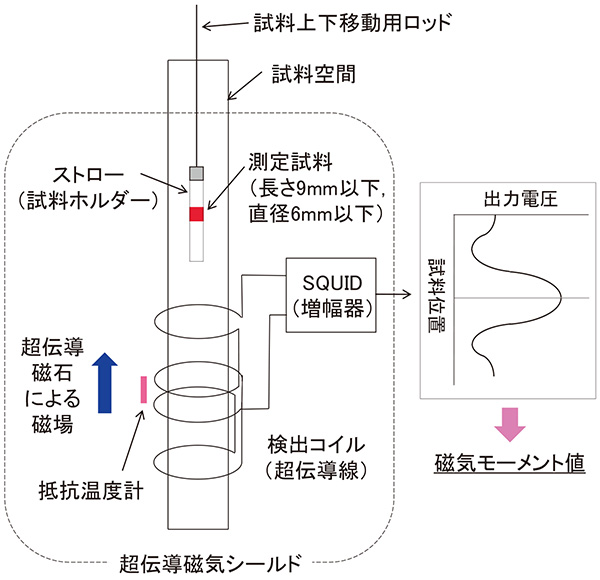
本研究で用いたSQUID磁束計の概略図。
Fig. 4はSQUIDで測定した各混合粉末試料の磁気モーメントの温度依存性測定結果である。電子天秤(最小表示0.01 mg)で秤量した各混合粉末試料の質量Wは21 mgから50 mgであり、80 K~ 340 Kの温度範囲で、1テスラに相当する磁界の強さHを試料に印加しながらmを測定した。試料中のGd2O3の「分析濃度」xanalを(1)式のnとGd2O3のモル質量、Gd2O3一分子あたりのGd3+イオンの数、アボガトロ定数より質量分率として求めた。Fig. 5にxanalと調製濃度xgravの比較結果を示す。
Fig.4
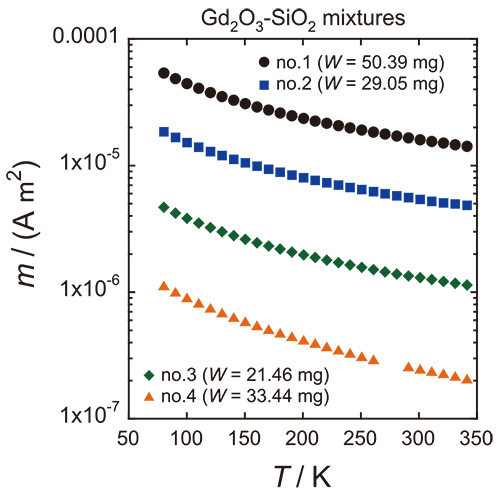
SQUID磁束計を用いたGd2O3-SiO2混合粉末試料の磁気モーメントの温度依存性測定結果。印加磁場は1 Tに相当。
Fig.5
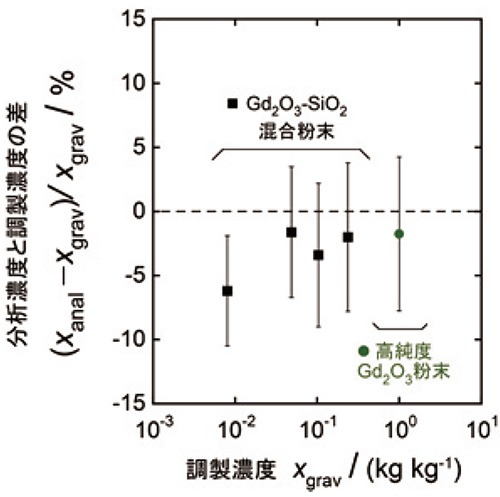
Gd2O3-SiO2混合粉末試料および高純度Gd2O3粉末試料を用いた本分析法の妥当性確認の結果。
最も低濃度であるno.4の試料を除くと、xanalとxgravの間には‒1.6% ~ ‒3.4%の差がみられる。各分析濃度の相対拡張不確かさは4 ~ 6%弱であり、不確かさの範囲内では一致している。xanalの不確かさへの寄与が大きい要因として、磁気モーメントの温度依存性測定のデータに対する回帰分析から得られるcCurieの不確かさu(cCurie)がある。この不確かさは測定温度範囲を液体ヘリウム温度付近まで拡張して、かつ、キュリー・ワイスの法則に従う磁気モーメントの温度依存性が保たれれば、約2%以下の相対不確かさまで小さくできる見込みである。u(cCurie)の大きな不確かさのもう一つの原因として、一定磁場・一定温度で同じ試料の磁気モーメントを繰り返し測定したときの再現性が現時点では良くない事が挙げられる。試料をSQUIDにセットして磁気モーメント値を繰り返し測定したときの相対標準偏差は0.01% ~ 0.4%と良好である。ところが、試料を一旦SQUIDの外に取出して、再びセットして測定すると、磁気モーメント値の変動が生じて相対拡張不確かさが約1.8%となる。この変動の原因を把握して、磁気モーメント測定値の不確かさを小さくしていく事は本研究の今後の課題の一つである。
有効磁気モーメントの理論値は自由イオンのランデのg因子gJ に基づいて算出されており、現実の結晶においては何らかのずれが生じている可能性が高い。これは、xanalとxgravの差の原因の一つであると考えられる。この問題の解決を試みる方法として、電子スピン共鳴(ESR)測定により混合粉末試料の実験値であるg値を求めることが考えられる。ESRスペクトルの横軸の情報である共鳴磁場B0とマイクロ波周波数νを、以下のESR基本方程式
hν = g μB B0···········(4)
に代入することにより、物理量の測定値と物理定数からg値gを直接求める(hはプランク定数である)。そして、式(2)のgJをgに置き換えれば、より精確な分析濃度が得られる可能性がある。ESR装置の汎用的なマイクロ波周波数であるXバンド(9.5 GHz)、および、より高周波数のバンド等によるESRスぺクトルの測定・解析を試みているところである。
安定フリーラジカルをもつ高純度有機化合物粉末の純度分析への適用
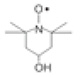
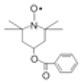
本分析法のアプリケーション開拓の試みとして、本分析法により、安定なニトロキシルラジカルをもつ数種類の高純度有機化合物粉末の「フリーラジカルとしての純度」の分析を試みた[10]。分析試料は、2,2,6,6-tetramethylpiperidine 1-oxyl [TEMPO]、4-hydroxy- 2,2,6,6-tetramethylpiperidine 1-oxyl [TEMPOL]、および、4-hydroxy-2,2,6, 6-tetramethylpiperidine 1-oxyl benzoate [安息香酸4-ヒドロキシ-TEMPO、4HTB]の市販の高純度粉末である。いずれも、ガスクロマトグラフ法の分析結果に基づき差数法または面積百分率法により算出された純度の情報が試薬メーカーにより提供されているものである。フリーラジカルを定量するため、(2)式のgJは、同じく理論値である自由電子のg因子ge [ = 2.0023 ]に置き換える。フリーラジカルのpの理論値は、J=S=1/2より1.7340である。しかしながら、上述の3種類の高純度有機化合物粉末の場合、いずれもXバンドESR装置により良好な一次微分スペクトルを測定できるため(4)式の実験値であるg値を用いた。Fig. 6は日本電子製JES-FA100で測定した安息香酸4-ヒドロキシ-TEMPOの高純度粉末のESRスペクトルである。この場合の分析手順のフローチャートをFig. 7に示した。 Table 2の分析結果において[10]、TEMPOL以外では、100%に近い純度の分析値が得られている。TEMPOLの純度が100%よりも約2%高い値となっているのは、この試料がFig. 8の通り、約6 Kで反強磁性転移を示す事と何らかの関連があるのではないかと推測している。各純度分析値の不確かさは、前述のGd2O3定量の場合と同様に、測定温度範囲の拡張等によって今後精度を向上できる見込 みである。また、いずれの試料においても、geをgに置き換えることにより、わずかではあるが純度が100%に近づく結果が得られており、本分析法におけるCW-ESR測定の効果である。現在、室温から液体ヘリウム温度近傍までにおいてもgが一定であることの確認をESRスペクトル測定により試みている[11]。
ESR測定自体、定量機器分析法の一つであり、高純度のESR用標準試料を溶液に溶解させることにより、標準液を調製して検量線を作成することが行われている。TEMPOLは代表的なESR用スピン量標準試料の一つである。生命科学分野のESR分析の参考書である文献[12]では、「ニトロキシルラジカルの純度は98%程度で、定量精度に心配がある場合は2種類以上の標準試料を併用して定量を行うと良い」とされている。本分析法により標準液調製の原料となる高純度有機化合物試料のフリーラジカルとしての純度を精確に定量できれば、その標準液で校正されたESRによるフリーラジカル定量結果の精確さ向上に寄与できるのではないかと考えている。
Fig.6
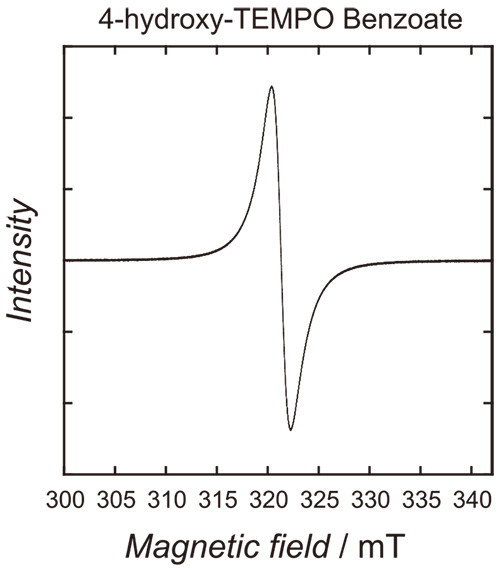
安息香酸4-hydrozy TEMPO高純度粉末のXバンドCW-ESR測定による一次微分スペクトル。
Fig.7
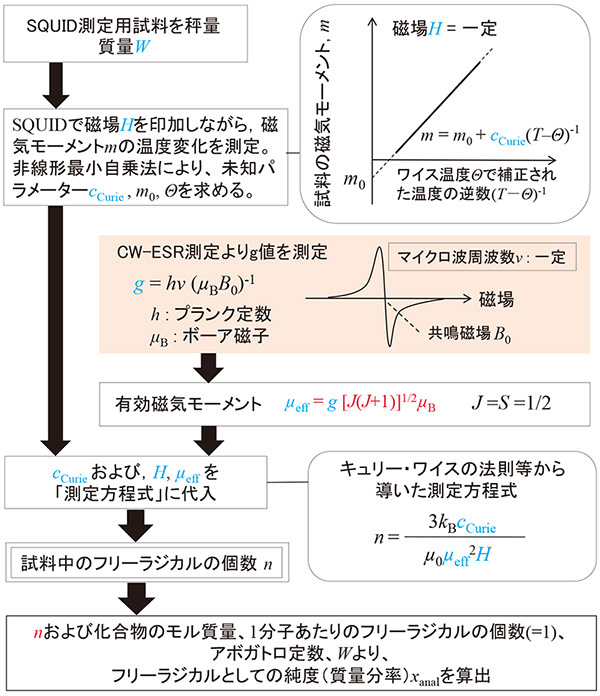
高純度有機化合物粉末のフリーラジカル純度の分析手順。—ESRの活用—
Table 2
| 化合物 | 試薬メーカーが公表している純度 (ガスクロマトグラフ分析による) |
有効磁気モーメント法によるフリーラジカルとしての純度の分析値 [100×(kg kg-1)] |
|
|---|---|---|---|
| 自由電子のランデのg因子geに基づく場合 | ESR測定によるg値gに基づく場合 | ||
TEMPO
 |
99.5 wt% | 100.3±6.4 (ge = 2.0023) |
99.8±6.4 (g = 2.0072 ±0.0002) |
TEMPOL
 |
99.5 wt% | 102.3±4.0 (ge = 2.0023) |
101.9±4.0 (g = 2.0069 ±0.0008) |
安息香酸 4-ヒドロキシ TEMPO (4HTB)
 |
98.5 wt% | 100.6±4.8 (ge = 2.0023) |
101.1±4.8 (g = 2.0071 ±0.0004) |
安定フリーラジカルをもつ高純度有機化合物粉末におけるフリーラジカルとしての純度の分析結果。各値は包含係数2の拡張不確かさを含む。
Fig.8
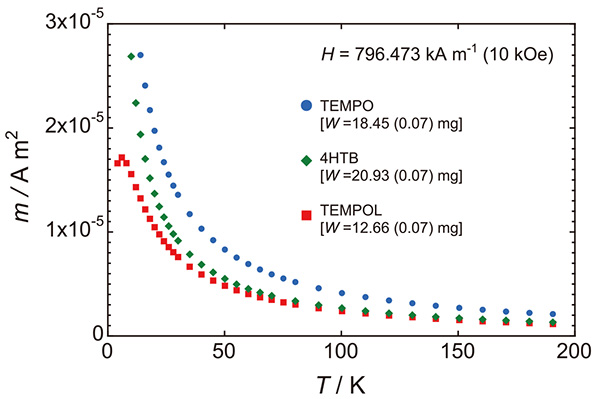
ニトロキシルラジカルをもつ高純度有機化合物粉末の磁気モーメントの温度依存性測定結果。
結論 (まとめ、おわりに)
濃度または純度が既知である標準物質を参照することなく定量が可能である本定量分析法は、分析化学便覧[13]による分析法の分類では、物理分析、非破壊分析、共存分析に該当する。また、現状の実験条件下では、試料の絶対量が10 ~ 100 mgの半微量分析、および、分析対象成分の相対量が1% ~ 100%の主成分分析(常量成分分析)に分類される。本分析法が適用できる試料の種類・濃度等は限られており、また、得られる分析値の不確かさも現時点では決して良いとは言えない。しかしながら、「(SI)→(一次標準直接法) →(一次標準比率法)→(純度・濃度が既知の標準物質による校正を必要とする機器定量分析法)→・・・」という川の流れがあるとするならば、その川の上流付近の川幅をほんの少しでも拡張させることができればと願いつつ、今後も本研究を発展させていきたい。
謝辞
本研究の一部は、文部科学省「ナノテクノロジープラットフォーム」事業の支援を受けて、産業技術総合研究所(産総研)ナノプロセシング施設において実施されました。磁気モーメントの温度依存性解析で使用した非線形最小二乗法プログラムは、産総研計量標準総合センターの下坂琢哉博士の自作によるものです。また、本研究はJSPS科研費 JP24750077の助成を受けたものです。本研究を進めている間にESRの活用を着想しましたが、産総研の小平哲也博士・水垣桂子博士、JEOL RESONANCEのESR関係者、ほか、ESRの専門家・経験者とのコミュニケーションによって、本研究におけるESRの活用が円滑に進みました。
なお、本稿は日本分析化学会誌「ぶんせき」2016年2月号に掲載された解説「キュリー・ワイスの法則に基づく定量分析法"有効磁気モーメント法"」[14]の一部を改訂したものです。
参考文献
- 石英夫、柘植新、角田欣一、原口紘き、"分析化学"、(1991)(丸善).
- 内山俊一編、"高精度基準分析法−クーロメトリーの基礎と応用−"、(1998)(学会出版センター).
- ISO Guide 35:2006, Reference materials – General and statistical principles for certification, 3rd ed., p 31, (2006).
- 井原俊英、齋藤剛、杉本直樹、シンセシオロジー、2(1)、12(2009).
- 三浦勉、ぶんせき、9、488 (2012).
- 太田恵造、"磁気工学の基礎 I−磁気の物理−"、第3章、共立全書(1973).
- Nobuhiro Matsumoto, Kenji Kato, Metrologia, 49, 530–537 (2012).
- Nobuhiro Matsumoto, Takuya Shimosaka, Accred. Quality Assur., 20, 115-124 (2015).
- Mike McElfresh, "Fundamentals of Magnetism and Magnetic Measurements Featuring Quantum Design’s Magnetic Property Measurement System", (1994), (Quantum Design, Inc. San Diego, CA).
- Nobuhiro Matsumoto, Takuya Shimosaka, J. Appl. Phys., 117, 17E114 (2015).
- Nobuhiro Matsumoto, Takuya Shimosaka, (Submitted to a journal).
- 河野雅弘、吉川敏一、小澤俊彦:"生命科学者のための電子スピン共鳴入門"、第2章、(2011)(講談社).
- 日本分析化学会編、改訂五版、分析化学便覧、第1章、(2001)、(丸善).
- 松本信洋、ぶんせき、2016(2)、63-67(2016).
