PFG-NMRにおける熱対流およびDouble Stimulated Echo (DSTE) 法

PFG- (Pulsed Field Gradient-) NMRは、分子やイオン (ここでは分子およびイオンの総称として粒子とよぶことにします) の自己拡散を扱います。特に溶液中での粒子の自己拡散を扱う場合、同じく粒子の並進運動を伴う液体の対流は、PFG-NMRの減衰データに直接的な影響を与えます。対流による粒子の並進運動が、自己拡散に対して無視できないほど大きい場合、信号減衰にコサイン様の変調が加わり、PFG-NMRから得られる"見かけ"の自己拡散係数が大きくなったり、減衰曲線が歪み時には負の位相の信号が得られたりします。DSTE (Double Stimulated Echo) 法 [1] は、PFG-NMRの信号減衰において、対流の影響を取り除くように設計されたパルスシーケンスです。

PFG-NMR

PFG-NMRでは、粒子の自己拡散を扱います。粒子の自己拡散は、熱エネルギーによるランダムなブラウン運動に由来するため、一定時間における粒子の変位は、ガウス関数からなる確率分布としてあらわすことができます。 PFG-NMRでは、Z軸方向の勾配磁場パルス (Pulsed Field Gradient; PFG) を用いて、Z軸方向の粒子の分布をエコー信号の強度としてエンコードします。ここで、Z軸方向の単位時間 t あたりの粒子のZ方向の変位Δzの確率分布 P(Δz,t) は式1で表すことができます (ここでDは自己拡散係数です)。

Figure 1に最も単純なPFG-NMR測定である、Pulsed Gradient Spin Echo (PGSE) のシーケンスを示します。PGSEのシーケンスは、スピンエコーのシーケンスをベースに、リフォーカスパルスを同じ強度のPFGで挟みます。リフォーカスパルスの働きにより、二つのPFGが逆向きに働きます。粒子が、二つのPFGの間に移動しない場合、一つ目のPFGで diphase された磁化は、二つ目のPFGで rephrase され、信号強度に変調は生じません (ただし、ここでは緩和による影響を無視しています)。しかしながら、二つのPFGの間で移動してZ軸方向に変位をもつ粒子の磁化は、完全にはrephase せず位相差が生じます (式2)。

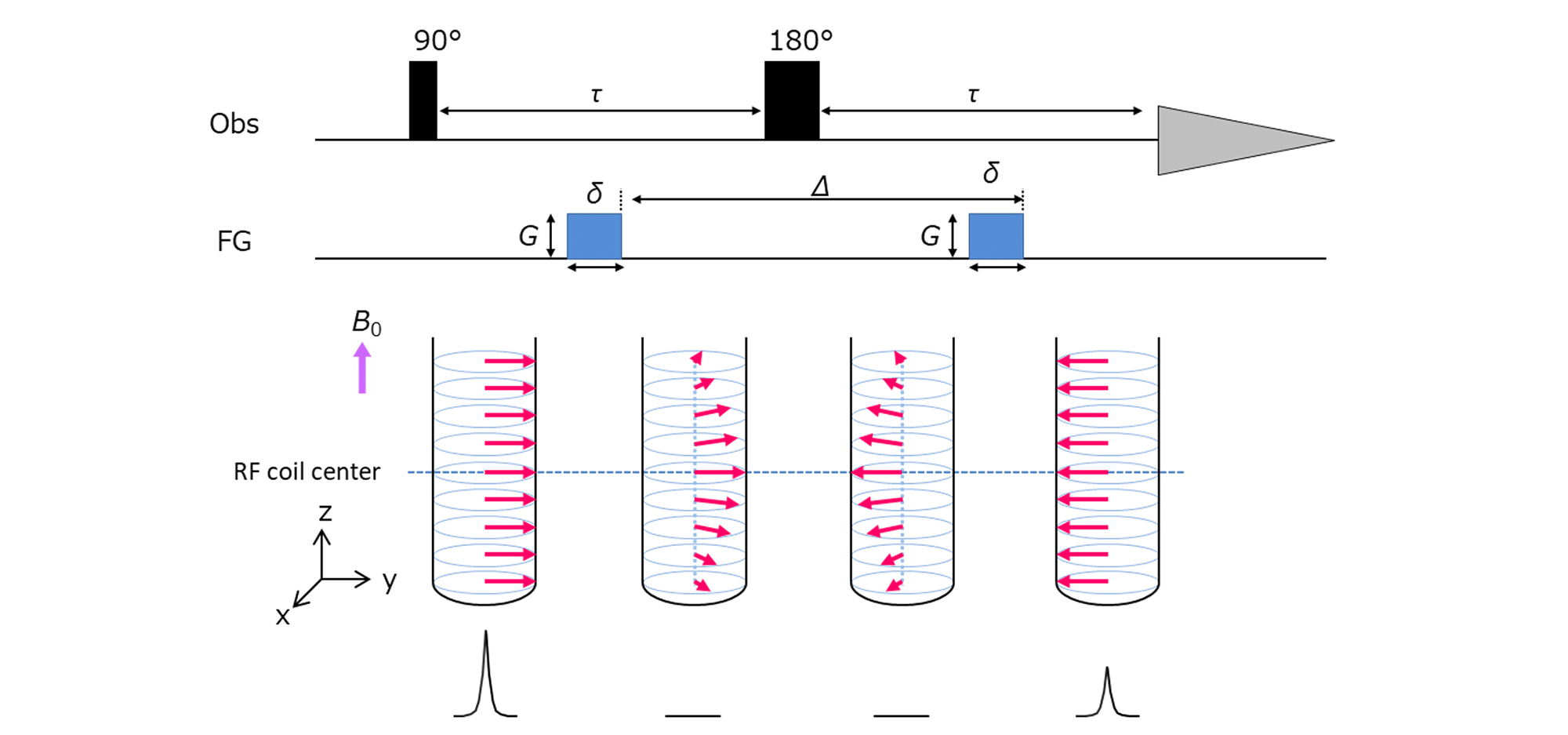
Figure 1 PGSEによる拡散時間における粒子のz軸方向の変位分布を信号強度変調としてエンコードの概略。

ここで、Z軸方向の変位は、式1の確率分布で表すことができることから、式1および式2に加え正規化することで式3の位相差の確率分布が得られます。ここで、γは核磁気回転比、GはPFGの勾配磁場強度、δはPFGのパルス幅、Δは拡散時間です。

ここで重要なのは、自己拡散による位相差の分布は平均が0であることです。ここで、位相の分布の広がりに応じて、信号強度の減少が観測されます。ここで、自己拡散による信号強度の減衰は、Stajskal Tannerの式として知られています [2] (式4)。

ここで、I_G=0 はG=0での信号強度、Δ* は実効拡散時間 [3] です。I(G) はGに関して (ハーフ) ガウス関数であり、G²に関しては、指数減衰関数になります。Gを変化させながら数点の信号強度を観測し、関数にフィッティングする、または逆ラプラス変換をおこなうことで自己拡散係数を分析することができます。

PFG-NMRにおける熱対流

NMR管内の溶液に温度勾配があると、温度勾配を駆動力として溶液が対流することがあります (熱対流)。Rayleigh-Bénard対流をNMR管のような長い円柱に拡張した場合、そのレイリー数は文献4によると式5で表すことができます [4]。

ここでgは重力加速度、αは熱膨張係数、κは熱伝導率、υは動粘度、γは溶液の半径、T*は軸方向の温度勾配です。一定のレイリー数 (臨界レイリー数) を超えると熱の輸送が、熱伝導では間に合わなくなり、溶液自体が運動する (対流) ことで熱の輸送がおこなわれます。熱対流を抑制するためには、試料の液高を小さくする (T*の減少、ミクロ試料管)、粘度の大きい溶媒を用いる (νの増大)、NMR管の内径を小さくする (γの減少、3 mm NMR管など) などが挙げられます。

ここでは、話を単純化するために、熱対流による粒子の移動が一定速度 (v) と仮定します。その時、拡散時間（PGSEにおける二つのPFGの間の時間）に生じる位相差は自己拡散のみのときは平均が0でしたが、熱対流による一定速度の粒子の移動では、その位相差の平均がずれることを意味します。したがって、文献[5] によると式6で表すようにコサイン様の変調が加わります。

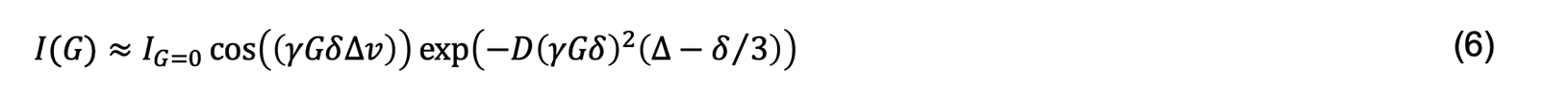
熱対流の影響を受けたPFG-NMRの初期の減衰データをStajskal Tanner式にフィッティングした結果得られる"見かけ"の自己拡散係数は、実際より大きくなってしまいます。以降は、vおよびDの大きさ次第になりますがコサイン様の変調は、Gaussianとの乖離がおおきくなり、減衰曲線は大きく歪み、場合によっては、得られる信号強度が負になります。

Double Stimulated Echo (DSTE) 法

(PG) DSTE法は、PFG-NMRにおける対流による望ましくない信号変調を取り除くために開発されたパルスシーケンスです [1]。DSTEの基本的なアイディアは、PFGを使ったエコーを2回繰り返しかつ２つのエコーを逆向きにすることで、それぞれのエコーにおける対流速度に依存した位相のずれを相殺します。具体的には、Figure 2(a) はシングルパルス実験に、2つのグラジエントエコーが導入されていますが、一つ目の+, -のエコーと二つ目の-, +のエコーでは、エコーが逆向きであるため、対流速度に依存した位相のずれが相殺されます。Figure 2(a) のシーケンスは、ただのグラジエントエコーなので、これに粒子のz軸方向の変位の分布をエンコードを組み合わせれば、熱対流による抑制を抑制したPFG-NMRシーケンスが得ることができます。
DSTE法では、PGSEの発展法である、Stimulated Echo (STE) を用います。STE法は、拡散時間のほとんどにおいて時間をz軸上に戻すため、PGSE法とくらべ横緩和の影響を受けにくく、また、同種核カップリングの変調の影響を受けません。DSTE法では、その名の通りstimulated echoを、シーケンスの中で2つ用います (Figure 2(b), V6: dste_led_diffusion.jxp)。PGDSTE法 (Figure 2(b))の4つのPFGでのコヒーレンス次数は、実線では、p=-1, +1, +1, -1のコヒーレンス次数となるように位相回しが設定されており、前の2つから構成されるエコーと後ろの2つから構成されるエコーが逆向きに設計されています。したがって、それぞれのエコーにおける対流速度に依存した位相のずれが相殺されます。両極性のPFGを使ったbipolar pulse pair (BPP) を用いたDSTE法 (BPPDSTE) も利用可能です (Figure 2(c), V6: bpp_dste_led_diffusion.jxp, V5: bpp_dste_led_dosy_pfg.jxp)。

DSTEおよびSTEの比較

熱対流が、STEにおいて自己拡散係数に影響すること、および、DSTEでその問題を解決できることを示す例をFigure 3に示す。4 w/v% polystylene (31 kDa, for GPC) がο-dichrorobenzene-d₄に溶解した試料を用い、90°Cにおいてパラメータをそろえて(Δ=200 ms，δ= 5 ms， G=30-270 mT/m) 測定しました。STEの信号減衰 (Figure 3 (a)) は、PGDSTEの信号減衰 (Figure 3 (b)) と比べて全体的に早いことがみてとれます。6.96 ppmの信号 (PStyの芳香族1H) の勾配磁場強度における強度減衰をFigure 3(c) に示します。ここでSTEの信号減衰は、Stajskal-Tannerの式から外れますが、 Stajskal-Tannerの式と比較的一致する減衰初期の強度をプロットしました。 Figure 3(c) においてその負の傾きが、自己拡散係数に相当しますが、STEから得られた自己拡散係数は"見かけの"自己拡散係数であり、DSTEから得られた実際の自己拡散係数とくらべ大きいことが分かります。また、STEから得られた"見かけの"自己拡散係数は、拡散時間に依存することがわかります (Figure 3(d)) [5]

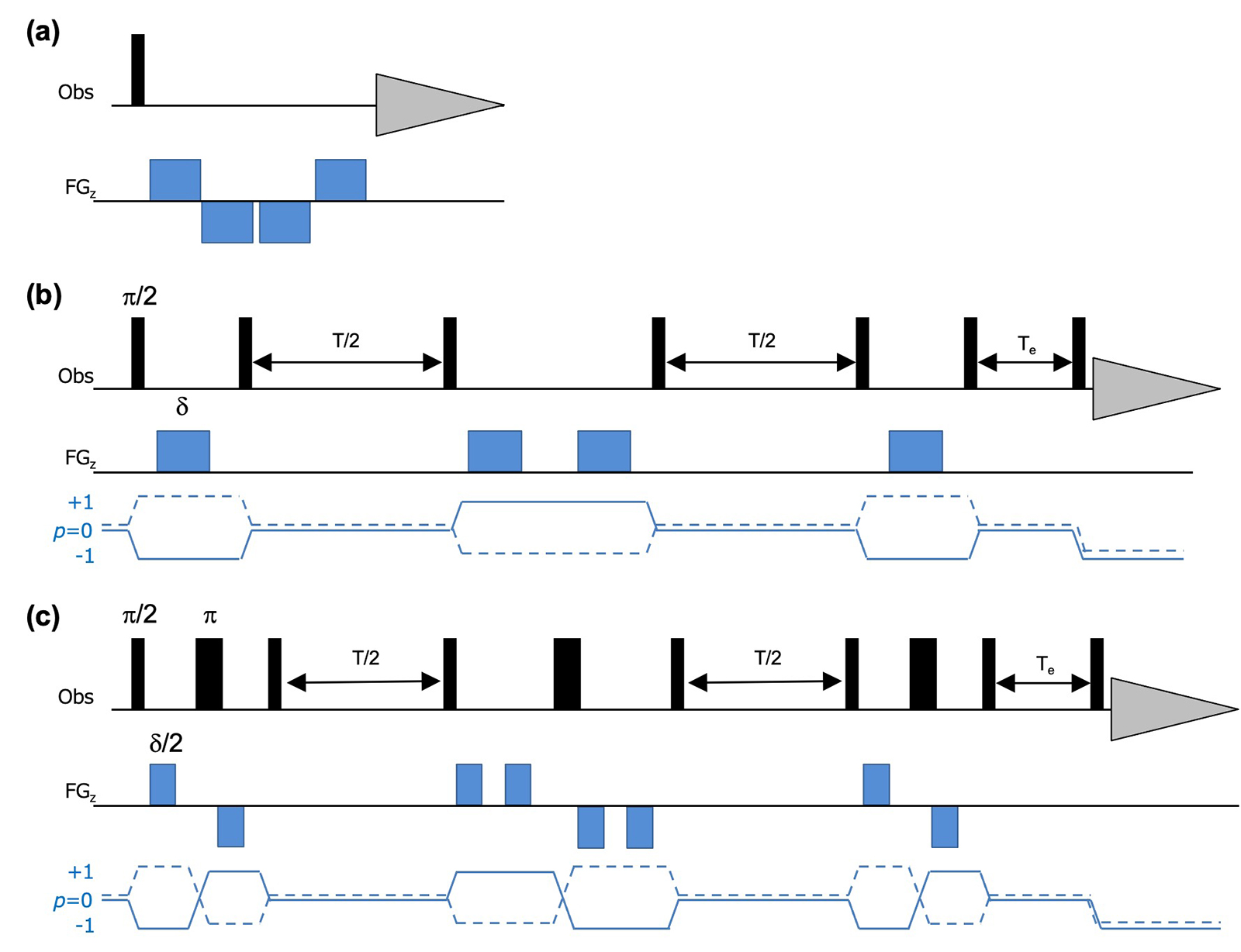
Figure 2 2つのエコーによる対流の影響を抑制。(a) ダブルグラジエントエコー、(b) DSTE (V6: dste_led_diffusion.jxp )、(c) BPP-DSTE ()、 V6: bpp_dste_led_diffusion.jxp、V5: bpp_dste_led_dosy_pfg.jxp)。Pは選択されるコヒーレンス次数を示す。

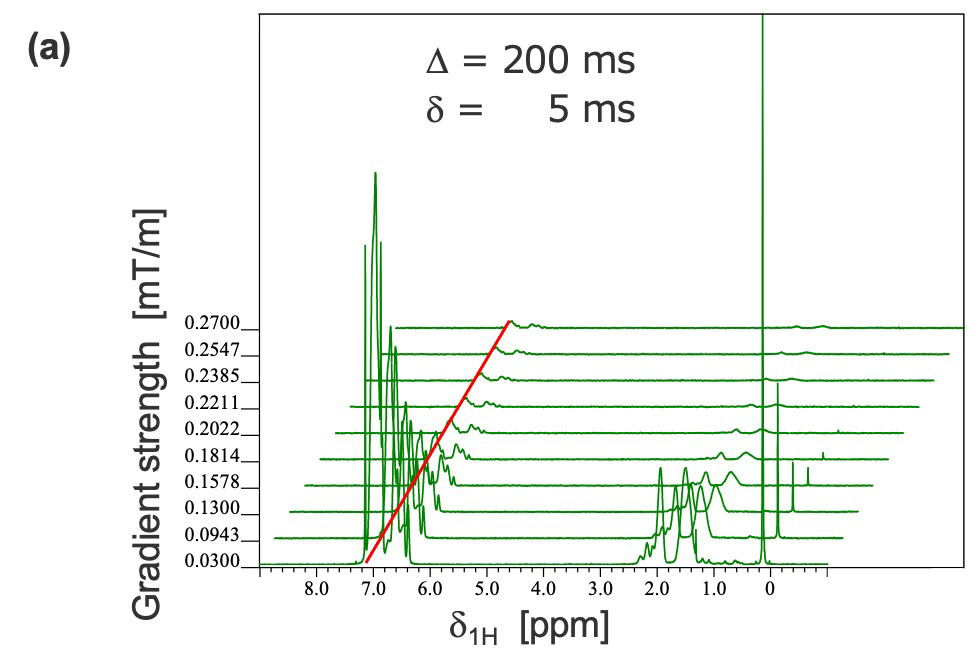
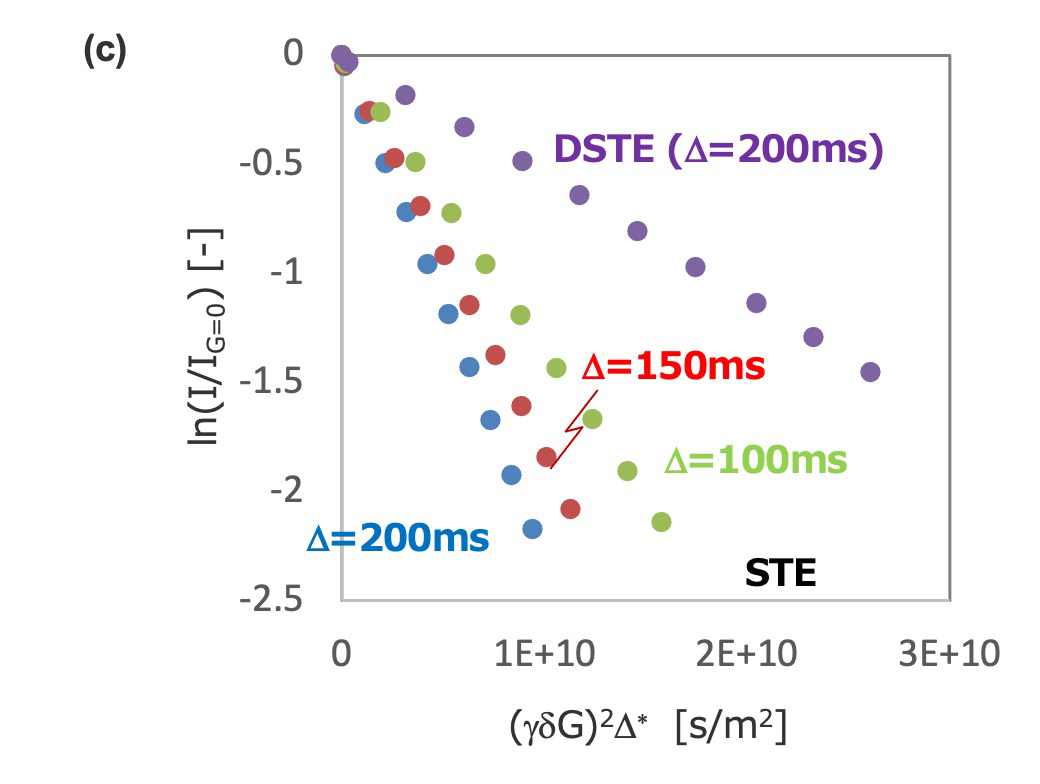
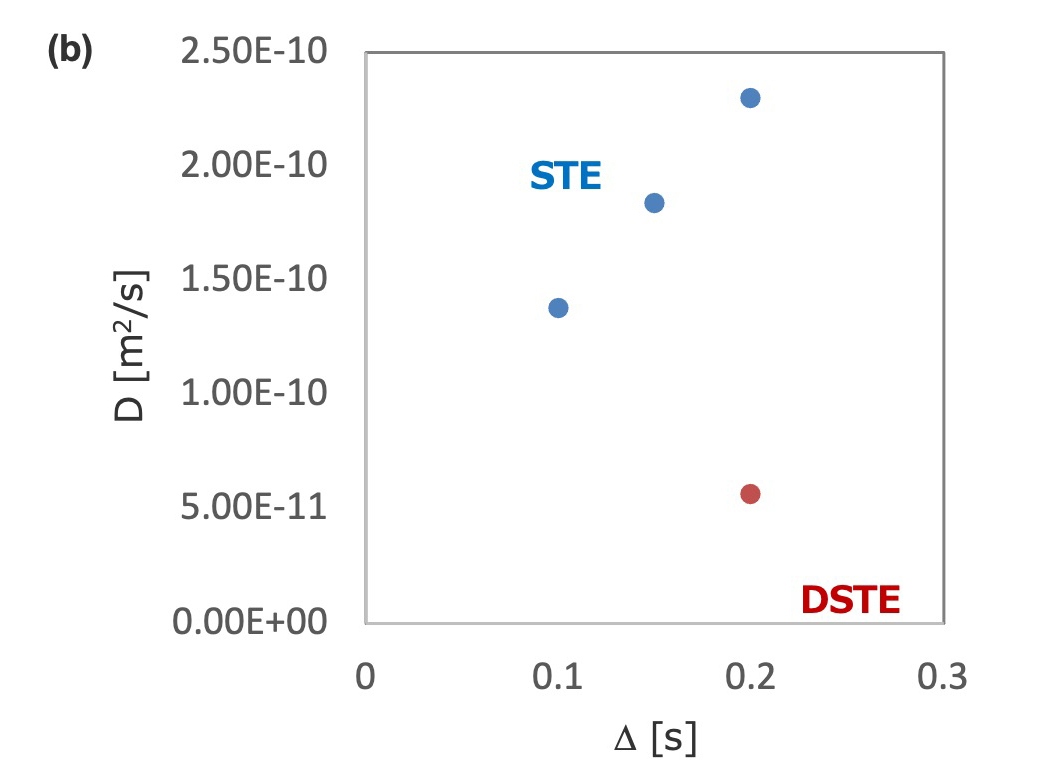
Figure 3 単分散ポリスチレンの90°CでのSTEおよびDSTEの比較。(a) STEおよびDSTE。拡散時間、PFG幅、強度などパラメータは統一したが、DSTEと比較しSTEの方が対流の影響で減衰が早い。(c) STEおよびDSTEにおける信号減衰をStajskal-Tannerの式にプロット。STEは、拡散時間が大きくなるほど、その負の傾きが大きくなり、みかけの自己拡散係数が大きくなる (d)。

一方、DSTEは、熱対流が生じている環境においても対流による信号強度変調を抑制することで、正確な自己拡散係数を得ることができます。本アプリケーションノートで示すように、DSTEは熱対流下でのPFG-NMR実験における強力なソリューションです。高温条件や、粘性が低い溶媒を用いたPFG-NMR実験では、 DSTEを検討する必要があるかもしれません。DSTEおよびSTEから得られた自己拡散係数を比較することで、熱対流が悪い影響を与えているか否かを診断することができます。

参考文献

[1] Jerschow, A., Muller, N., “Suppression of Convection Artifacts in Stimulated-Echo Diffusion Experiments. Double-Stimulated-Echo Experiments” J. Magn. Reson., 125 (1997) 372-375.

[2] Stejskal, E.O., Tanner, J.E., “Spin diffusion measurements: Spin echos in the presence of a time-dependant field gradient”, J. Chem. Phys., 42 (1965) 288-292.

[3] Sinnaeve, D., “The Stejskal–Tanner Equation Generalized for Any Gradient Shape—An Overview of Most Pulse Sequences Measuring Free Diffusion” Concept. Magn. Reson., 40A (2012) 39-65.

[4] Claridge, T.D.W, “Diffusion NMR Spectroscopy” in High-resolution NMR techniques in organic chemistry 3rd edition, Amsterdam, Nederland: Elsevier B.V.　

[5] Hedin, N., Yu, T. Y., Furó, I., “Growth of C12E8 Micelles with Increasing Temperature. A Convection-Compensated PGSE NMR Study” Langmuir, 16 (2000) 7548-7550.

印刷用PDF (1 MB)