Diffusion Analysis Multi —多成分指数減衰関数によるPFG-NMR減衰データのフィッティング—

PFG- (Pulsed Field Gradient-) NMRは、分子やイオンの自己拡散を扱います。 PFG-NMRでは、PGSE法 (Pulsed Gradient Spin Echo) やPGSTE法 (Pulsed Gradient STimulated Echo) において、一般的にはPFGの勾配強度を数点変化させるアレイ実験をおこない、得られたアレイデータにおける各信号の減衰をモデル式にフィッティングすることで自己拡散係数を分析します。Delta NMRソフトウェアの回帰計算ツールでは、PFG-NMRの減衰データをモデル式にフィッティングし、自己拡散係数を推定する機能を有します。Delta NMRソフトウェア Ver. 5.3.3以前は、同じ化学シフトに単一の自己拡散係数が存在することを想定したモデル式のみ対応していました。同じ化学シフトに複数の自己拡散係数がある場合を想定した、"Diffusion Multi"モードが、Delta NMRソフトウェア Ver. 6.0より実装されました。

背景

PFG-NMRにおいて、注目する信号が単一の自己拡散係数をもつ成分に由来する場合、得られる信号強度I(G) は、以下のStajskal Tannerの式 [1] にしたがいます。

ここで、I_G=0, γ, G, δ, およびΔ*は、それぞれG=0の時の信号強度、用いた核の磁気回転比、PFGの磁場勾配、PFG-NMR実験における勾配磁場パルス幅、および実効拡散時間 [2]です。そのため、数点の勾配磁場強度から信号の減衰を観測し、 Stajskal Tannerの式にフィッティングすることで、自己拡散係数Dを求めることができます。ここで、I(G) はGに関してはガウス関数ですが、G²に関しては指数減衰関数です。
　自己拡散係数を求めたい信号が単一の自己拡散係数をもつ成分に由来する場合、両辺の自然対数をとることで、次式のように変形でき、単純な線形回帰問題として自己拡散係数を分析することができます。このとき、(γGδ) ²Δ*に対するln(I(G)/I_G=0)の負の傾きの大きさが、自己拡散係数に相当します。

一方、自己拡散係数を求めたい信号に、複数の自己拡散係数が離散的に存在する場合、式3のように多成分に拡張したモデル式を用いる必要があります。

ここで、jは同じ化学シフトに含まれる自己拡散係数の数です。単一の自己拡散係数を想定したモデル式の場合のように、両辺の自然対数をとって線形回帰問題に持ち込むことはできません。そのため、多成分に拡張したモデル式の場合、I_{G=0, i} およびD_iを数値解として推定します。この非線形最小問題から数値解を得るためには、 I_{G=0, i} およびD_i の初期値を設定する必要があり*、かつ、得られる数値解は、初期値に依存することがあることに注意が必要です。同じ化学シフトに複数の自己拡散係数がある場合を想定した、"Diffusion Multi"モードが、Delta NMRソフトウェア Ver. 6.0以降の回帰計算ツールに実装されましたので、次セクションでは、その手順を説明します。

分子量の異なる単分散ポリスチレン混合溶液を用いた"Diffusion Multi"モードのチュートリアル

"Diffusion Multi"モードを使った複数の自己拡散係数の回帰計算のチュートリアルとして、分子量の異なる単分散ポリスチレン混合溶液のPGSTE 法による減衰データを用いました。具体的にはMw: 3510 DaおよびMn: 3350 Daの単分散ポリスチレンおよびMw: 35400 DaおよびMn: 34400 Daの単分散ポリスチレンを等重量で混合した4 wt%のo-dichlorobenzene-d₄溶液を試料に用いました。

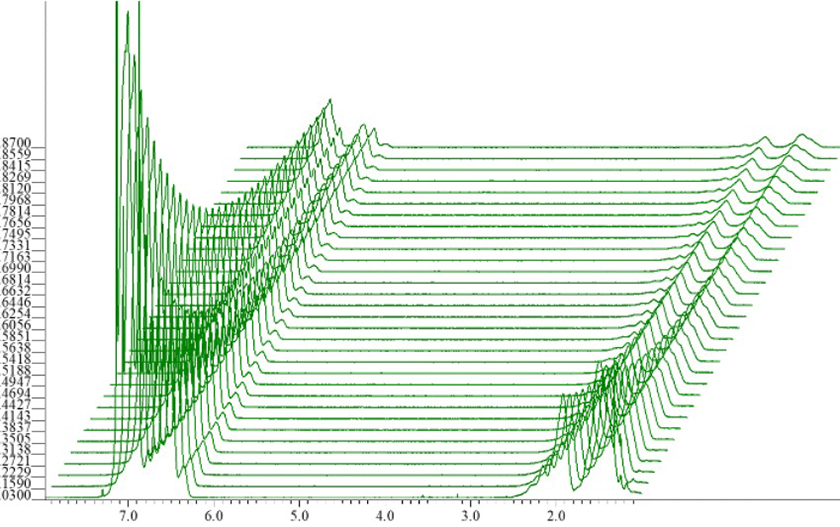
Figure 1 分子量の異なる単分散ポリスチレン混合溶液 (Mw: 3510 DaおよびMn: 3350 Daの単分散ポリスチレンおよびMw: 35400 DaおよびMn: 34400 Daの単分散ポリスチレンを等重量で混合した4 wt%の重水素化o-dichlorobenzene-d₄溶液) のPGSTEの減衰データ

測定されたアレイデータのx軸の処理をします。フーリエ変換および位相を補正したデータをFigure 1に示します（表示モードをスタックにしています、ショートカットキーは"4")。データスレートのツールバー->解析ツール->回帰計算ツールから回帰計算解析ツールを開きます。「回帰計算解析」ウインドウの［ピーク］をクリックして、ピークモードに変更します。 [ピークモードボタン]もしくは [自動ピークピックボタン]から自己拡散係数を計算したい信号をピークピックし、カーソルで選択します。「回帰計算解析」ウインドウのモードのパラメータを「Diffusion Analysis Multi」に変更します。そのまま実行ボタンを押すと一成分の自己拡散係数を含む3式 (j=1) として、フィッティングをおこないます。しかしながら、今回のデータは同一化学シフトに2つの自己拡散係数 (D₁, D₂) を含む3式 (j=2) をモデル式に採用したいため [計算パラメータを追加ボタン] を押して計算パラメータを追加します。 [計算パラメータを追加ボタン]を押すと、[1]D, [1]I(0), [2]D, [2]I0の4つの未知変数の入力ボックスが表示されます (Figure 2)。これらの未知変数は、それぞれ、1成分目の自己拡散係数、 1成分目の自己拡散係数の初期強度、 2成分目の自己拡散係数、および2成分目の自己拡散係数の初期強度を示します。これらに推定される自己拡散係数および初期強度を入力して*, **実行ボタンを押します（見当がつかないときは、1成分のフィッティングを実行し、そこで得られた値を少し変化させるとよいでしょう。 1成分のフィッティングでは内部的に初期値を設定するため初期値を設定する必要はありません）。

* ここで自己拡散係数は数値のみ入力します。単位は[m2/s]になります。
** 指数の形式で入力できます (ex. 9.9e-10)。しかしながら、小数点第一桁まで入力する必要があります(1.0e-11<-OK, 1e-11<-NG)。

Figure 2 回帰計算解析ツールの「Diffusion Analysis Multi」によるPFG-NMR減衰データの多成分フィッティングの手順

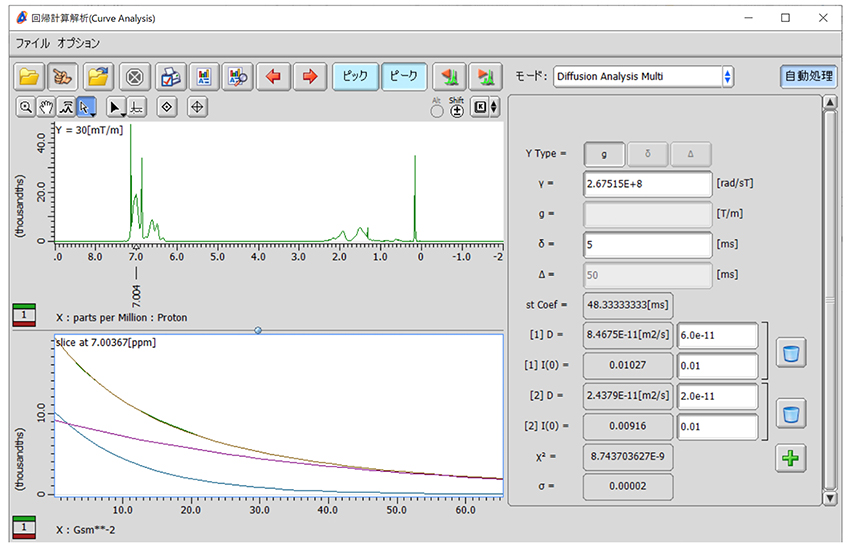
Figure 3 分子量の異なる単分散ポリスチレン混合溶液 (Mw: 3510 DaおよびMn: 3350 Daの単分散ポリスチレンおよびMw: 35400 DaおよびMn: 34400 Daの単分散ポリスチレンを等重量で混合した4 wt%の重水素化o-dichlorobenzene-d₄溶液) のPGSTEの減衰データのDiffusion Analysis Multiによる2成分フィッティング。例として7.00 ppmの信号の減衰曲線を用いた

Figure 3に「Diffusion Analysis Multi」モードでの分析結果を示します。ここでは、分子量の異なる単分散ポリスチレン混合溶液のPGSTE 法による減衰データの7.00 ppmの信号 (ポリスチレンの芳香族水素) を[1]D, [1]I(0), [2]D, [2]I0の初期値が、それぞれ、6.0e-11, 0.01, 2.0e-11. および0.01で分析をおこないました。分析より、8.47e-11および2.44e-11 m²/sの自己拡散係数が、0.0103:0.0092の割合であると推定されました。また、フィッティングから得られた結果と、実測の減衰曲線との一致の指標としては、カイ二乗値 (χ²) および標準偏差 (σ) が計算され表示されます。また、このとき、回帰計算解析ツールの左下の減衰データ表示部は、横軸が (γGδ)²Δ*となり信号強度は指数減衰となります。レイヤー1 (既定値では緑) が実測減衰データ、レイヤー2 (既定値では茶) がフィッティングされたモデル (＝すべての成分の和)、レイヤー3 (既定値では紫) 以降がそれぞれの自己拡散係数成分の減衰曲線になり、視覚的にフィッティングの結果を確認できます。
　この分析は、数値的に解いているため、特に初期値が実際の値と解離している場合、実際の値と異なる局所最適解に陥る可能性があることに注意が必要です。また、特に測定データ (減衰曲線) にノイズや誤差大きいとき、また、求めたい自己拡散係数の差が小さいときは、数値解が不安定になりやすいことに注意が必要です。また、自己拡散係数の数が未知なとき、その自己拡散係数の成分数を推定するときも注意が必要です。一般に、多成分フィッティングでは、フィッティングに使う成分数が多い方が、実測データとの一致度はよくなり、残差は小さくなります (つまりカイ二乗値および標準偏差が小さくなる) が、そのことは、モデル (の成分数) が実際の成分数と一致するとは限りませんので、適切な成分数は慎重に検討する必要があります。

参考文献

[1] Stejskal, E.O., Tanner, J.E., “Spin diffusion measurements: Spin echos in the presence of a time-dependant field gradient”, J. Chem. Phys., 42 (1965) 288-292.

[2] Sinnaeve, D., “The Stejskal–Tanner Equation Generalized for Any Gradient Shape—An Overview of Most Pulse Sequences Measuring Free Diffusion” Concept. Magn. Reson., 40A (2012) 39-65.

印刷用PDF (771 KB)