断熱パルス (Adiabatic Pulse)

はじめに

近年の高磁場NMRにおいて、¹³Cなどの広い化学シフト幅を持つ核の全ての信号を通常の矩形波パルスによって励起することは難しくなってきた。その問題を解決するために広帯域パルスと呼ばれる技術が開発されてきた。広帯域パルスは現在使用されている多くのパルスシーケンスの多くに組み込まれており、現代のNMRにおいて重要な要素の一つと言える。本アプリケーションノートでは広帯域パルスの一つ、断熱パルス (Adiabatic Pulse)、そのうちCHIRPパルス、WURSTパルス、CHIRP compositeパルスについて説明する。

位相変調と周波数変調

ラジオ波Rは式1のように周波数ω、位相ϕ、定数A、時間tによって規定される。

ここで、位相ϕを時間依存的に変化させることを考える。ここでは簡単のために位相は線形に変化するとする (式2) 。

式2を式1へと代入すると次のようになる (式3) 。

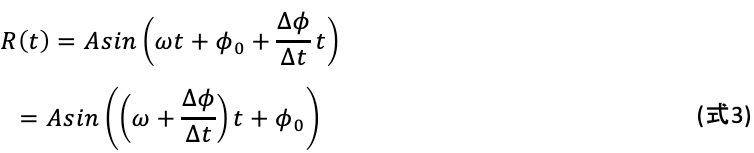
式1と式3を比較すると、周波数がωからω+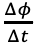へと変化していることが分かる。このようにラジオ波の位相を変化させることで実質的に周波数を変化させることが可能であり、断熱パルスを含め広帯域パルスではこの仕組みを用いて広い帯域の励起を達成している。

CHIRPパルス

CHIRPパルスは断熱パルスのうちの一つであり、ラジオ波の強度の立ち上がりと終わりをサインカーブとし、位相を大きく変化させたパルスのことを指す (Fig. 1)。CHIRPは周波数を掃引するという意味の用語である。このように位相を変化させることで実質的に周波数を掃引して励起することが可能である。Fig. 2に矩形波inversionパルスを用いた場合とCHIRPパルスを用いた場合の励起プロファイルを示す。CHIRPパルスを用いた場合、矩形波を用いた場合と比較して極めて優れた励起範囲とラジオ波強度のずれへの耐久性を持つということが分かる。周波数を増加させるCHIRP+と周波数を減少させるCHIRP-の二つがある。

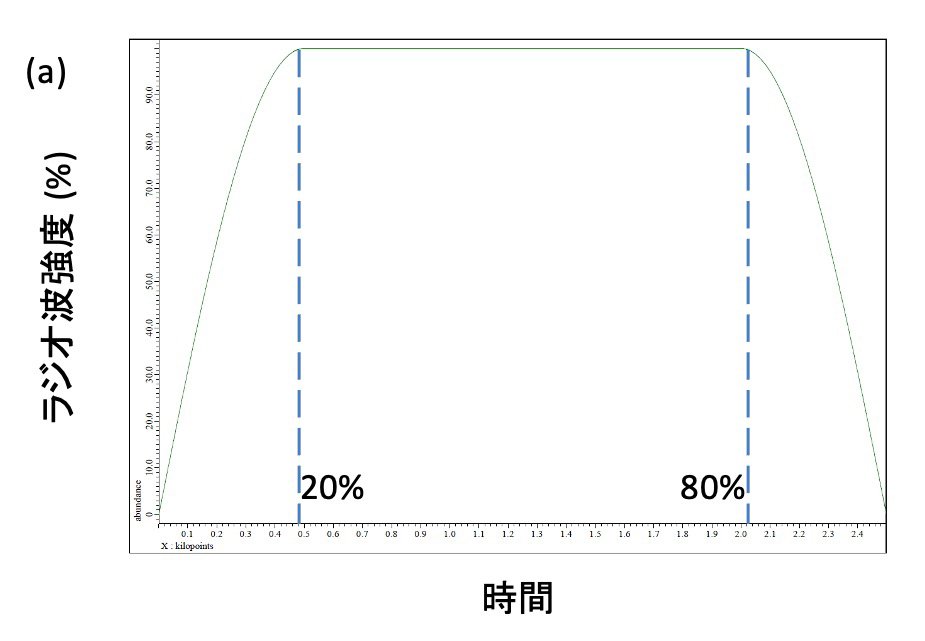
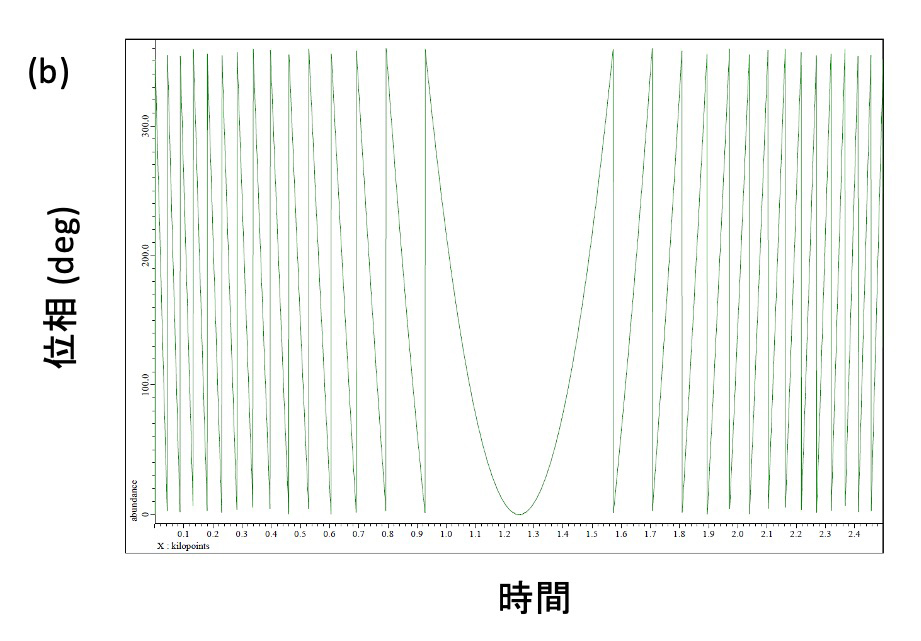
Figure 1 CHIRPパルスのラジオ波強度 (a) および位相 (b) の時間変化
ラジオ波の立ち上がりと終わりの20%がサインカーブになっている。位相を大きく変化させることで実質的に周波数を掃引する。

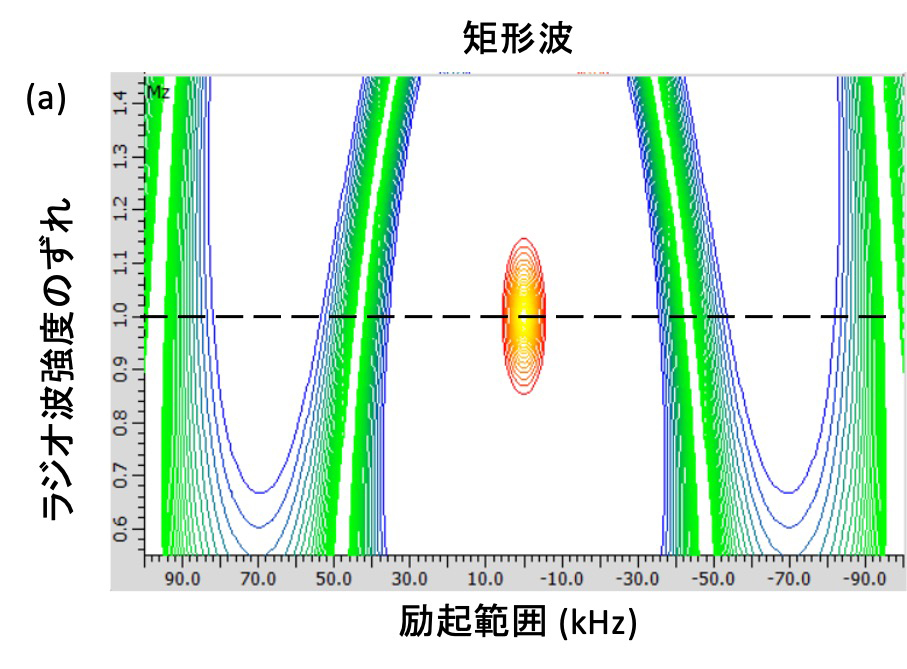
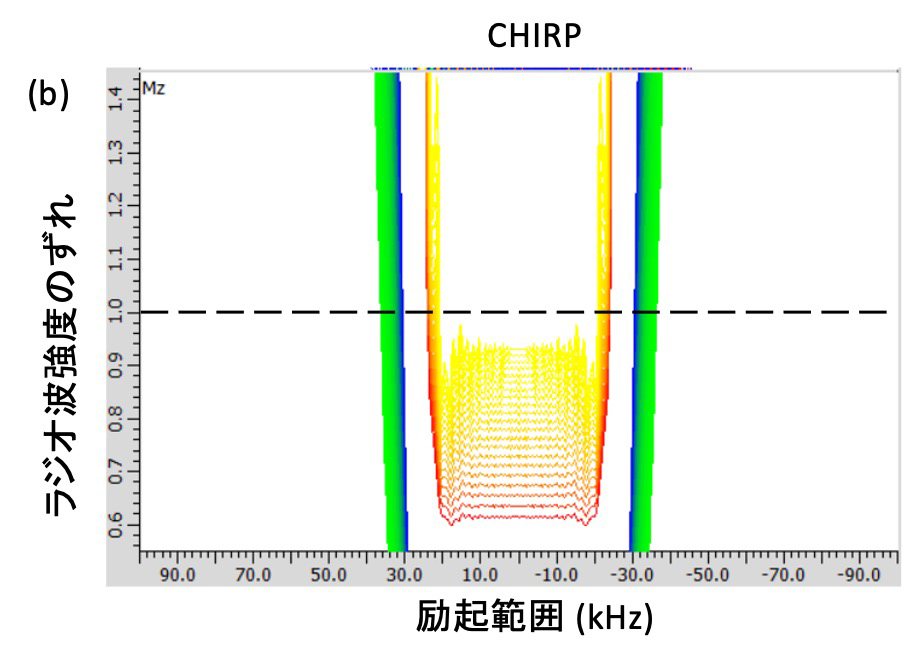
Figure 2 矩形波inversionパルス (a) とCHIRPパルス (b) の励起プロファイル
CHIRPパルスは矩形波パルスより優れた励起プロファイルを持つ。

WURSTパルス

WURSTパルスはWideband, Uniform Rate, and Smooth Truncationの略であり、CHIRPパルスと同様にinversionパルスとして機能する。CHIRPパルスとの違いは、ラジオ波強度が式4の形になっていることである。

nには通常20の値を入れるが、nの値によって励起効率はほとんど変化しない。Fig. 3 にWURSTパルスのラジオ波強度の変化と位相の変化を示す。CHIRPよりパルスの立ち上がりと終わりが滑らかになっている。励起効率は対応するCHIRPパルスとほとんど変わらない。周波数を増加させるWURST+と周波数を減少させるWURST-の二つがある。

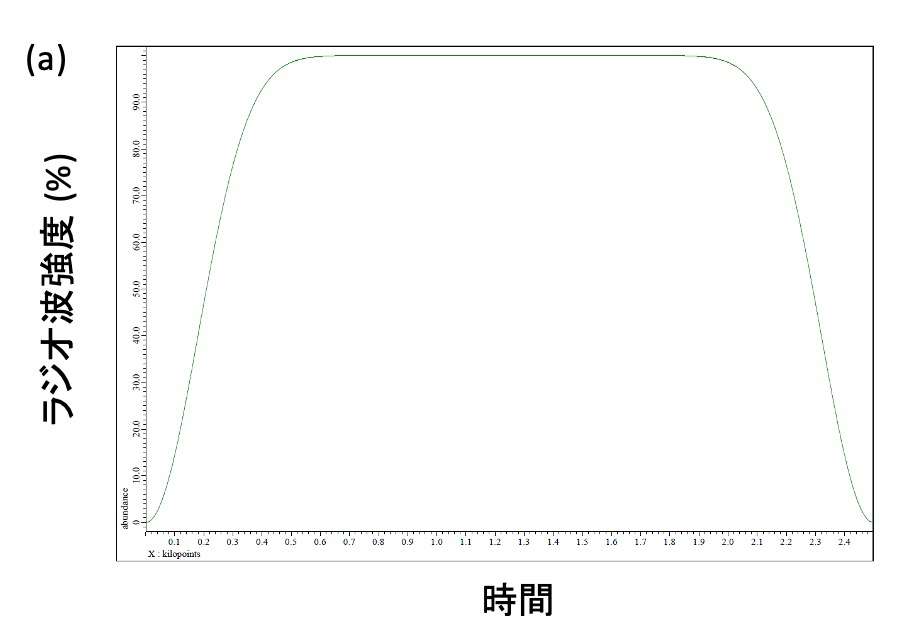
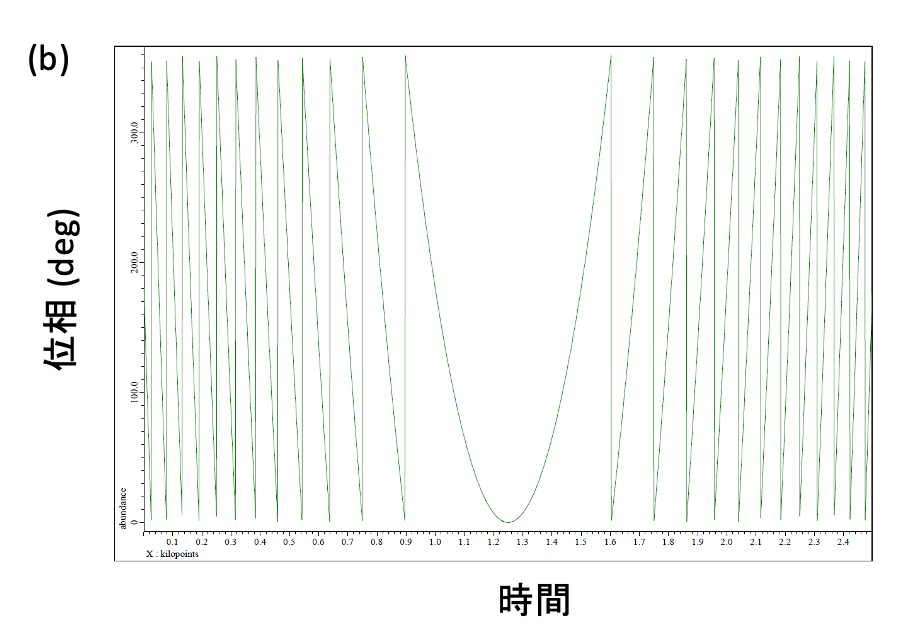
Figure 3 WURSTパルスのラジオ波強度 (a) および位相 (b) の時間変化を示す。
ラジオ波強度は1−((sin⁡(βt))ⁿの形の時間変化となっている。

断熱パルスのパラメータ

断熱パルスは以下の4つのパラメータによって規定される。

• ΔF 励起範囲 (周波数を掃引する範囲)、10-100kHzの値を入力する。この値の約80%が励起範囲となる。

• T パルス幅、0.5 – 5.0 msの値を入力する

• Q 断熱パルスのラジオ波強度を決定するパラメータ (adiabatic factor)。flip angle (β) が 180 degにて発散するような関数 (式5) となっている。180度パルスとして用いる場合には5以上の値であればよい。

• R ラジオ波強度。式6によって決定される。

実際に断熱パルスを用いる際にはΔF, T, Q, Rの順番にパラメータを設定する。

各パラメータの関係は以下のようになっている。

①パルス幅 T とadiabatic factor Q が固定されているとき
T および Q が固定されているとき、ラジオ波強度 R は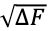に比例して大きくなる。

②励起範囲 ΔF とadiabatic factor Q が固定されているとき
ΔF および Q が固定されているとき、ラジオ波強度 R は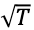 に反比例する。

③励起範囲 ΔF とパルス幅 T が固定されているとき
ΔF および T が固定されているとき、ラジオ波強度は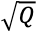に比例して大きくなる。ΔF = 80 kHz、T = 2 ms にて固定し、Q を3, 5, 8, 10と変化させたときの励起プロファイルをFig. 5 に示す。adiabatic factor Q が大きくなるとラジオ波強度 R が大きくなり、同時にラジオ波強度のずれへの耐久性も大きくなる。

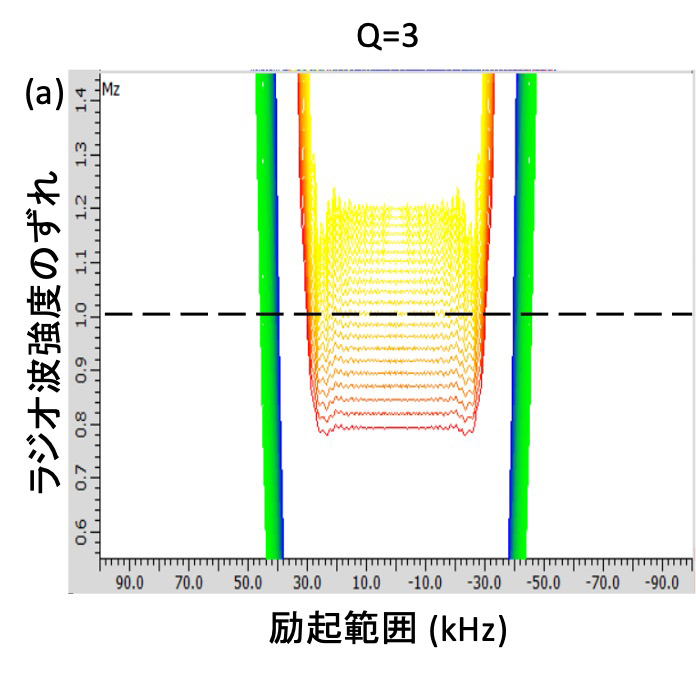
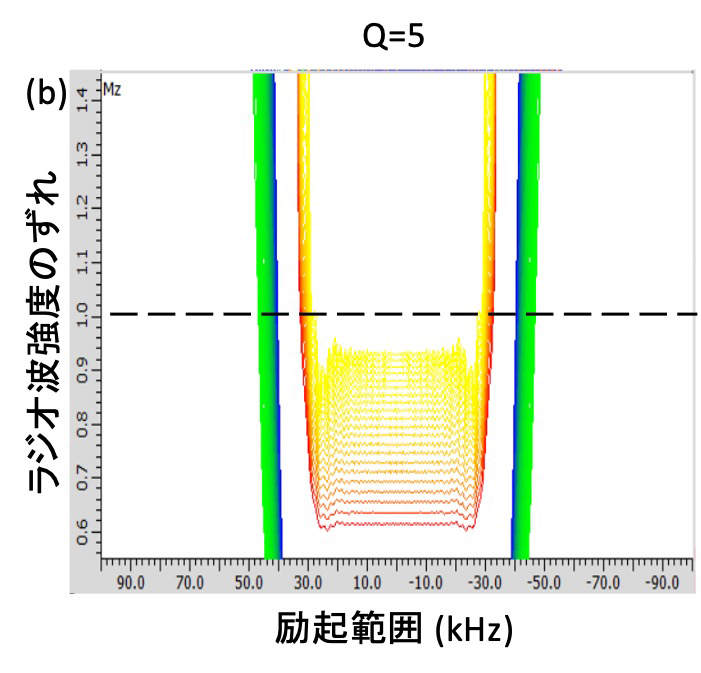
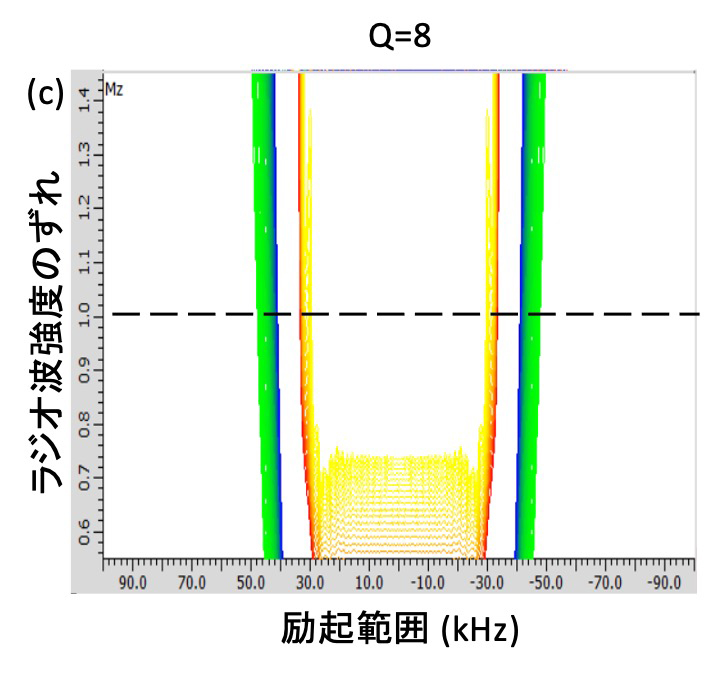
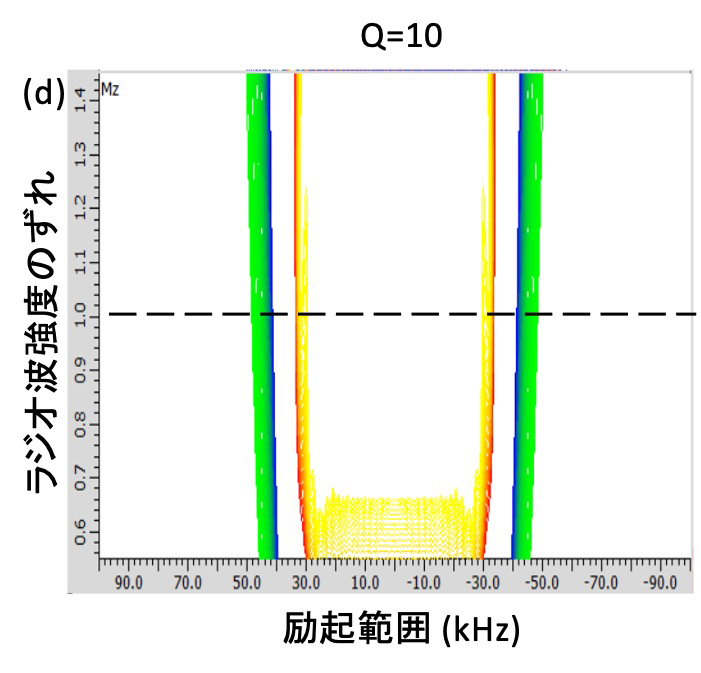
Figure 4 CHIRPパルスのQおよびRを変化させた場合の励起プロファイル
ΔF = 80 kHz、T = 2ms にて固定し、(a) Q = 3, R = 4.4 kHz (b) Q = 5, R = 5.6 kHz (c) Q = 8, R =7.1 kHz, (d) Q = 10, R = 8.0 kHz としている。Qを大きくするとRも大きくなり、同時にラジオ波強度のずれへの耐久性も大きくなることが分かる。

CHIRPパルスをrefocusパルスとして用いると

CHIRPパルスおよびWURSTパルスはinversionパルスとしてのみ機能し、同じ180degパルスであるrefocusパルスとしては機能しない。Fig. 5にCHIRPパルスをinversionおよびrefocusパルスとして用いたときの励起プロファイルを示す。このように、refocusパルスとしては正しく機能しない。

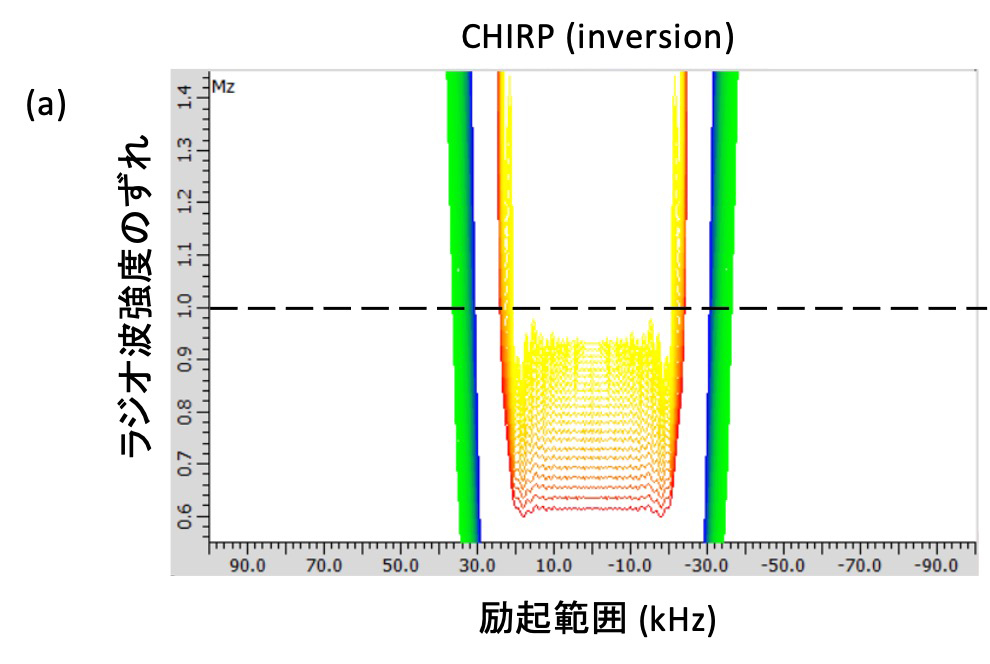
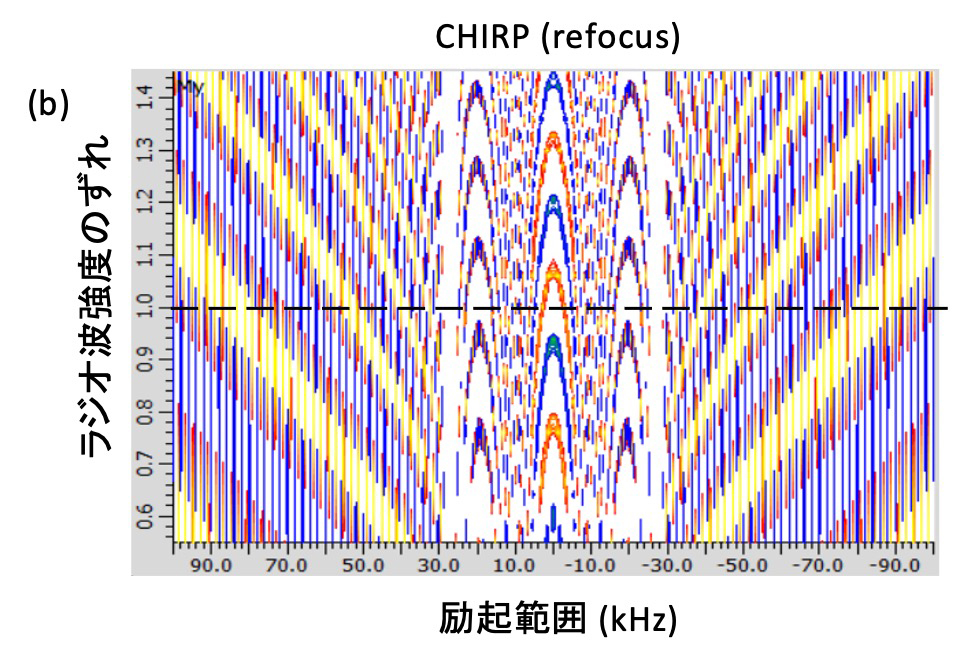
Figure 5 CHIRPパルスを (a) inversion (b) refocusパルスとして用いた場合の励起プロファイルを示す。
このように断熱パルスはinversionパルスとしてのみ機能し、refocusパルスとしては機能しない。

CHIRP Compositeパルス

CHIRP CompositeパルスはCHIRPパルスを3つ組み合わせたパルスであり、Fig. 6のようにラジオ波強度および位相を変化させている。これにより、inversionパルスとrefocusパルスの両方として用いることが可能となる。弊社NMR解析用ソフトウェアDelta (ver6.0以降) にはchirp_com_60_2m, chirp_com_80_2m, chirp_com_100_2mの3つが搭載されている。矩形波パルスおよびchirp_com_60_2mの励起プロファイルをFig. 7に示す。inversionとrefocusの両方として優れた励起プロファイルを示すことが分かる。

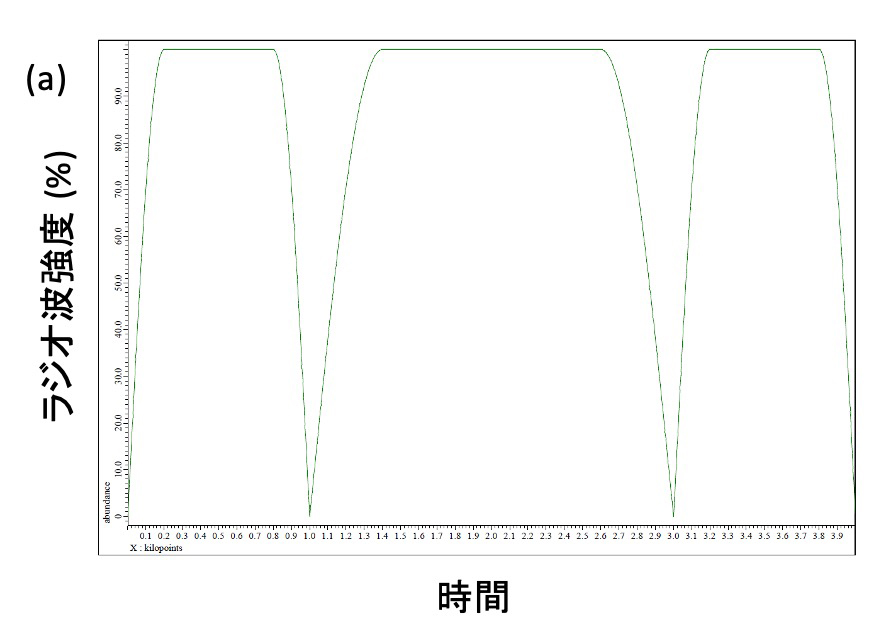
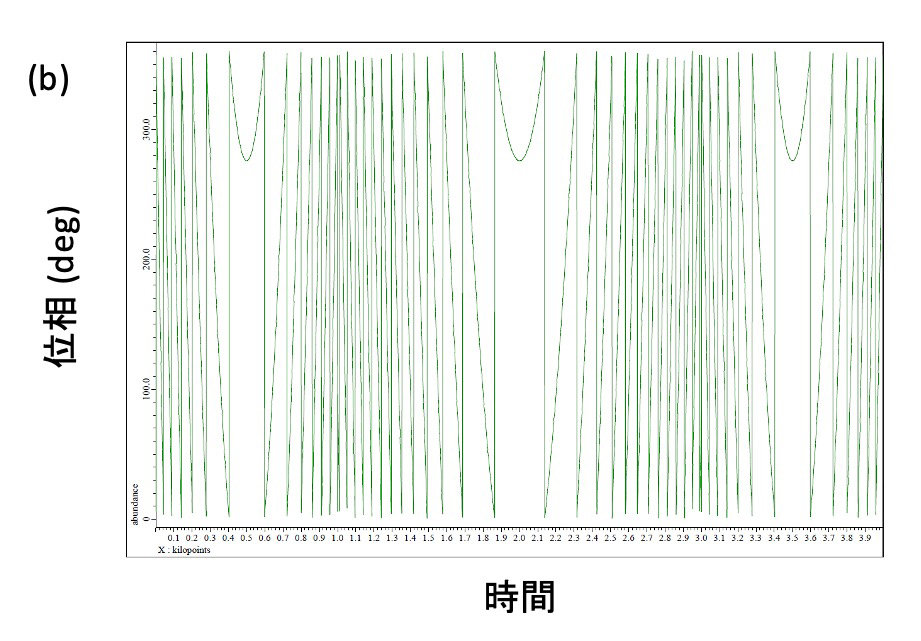
Figure 6 CHIRP Composite パルスのラジオ波強度 (a) および位相 (b) の変化。
3つのCHIRPパルスを組み合わせている。

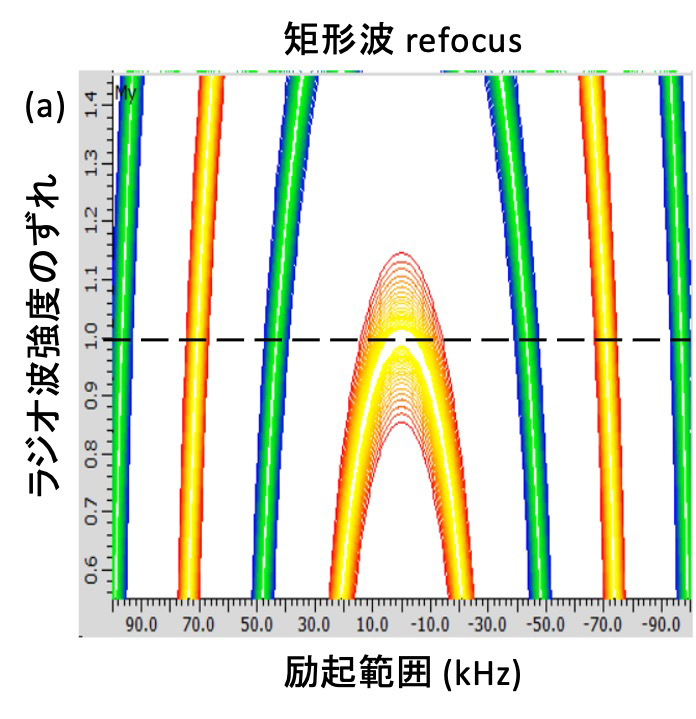
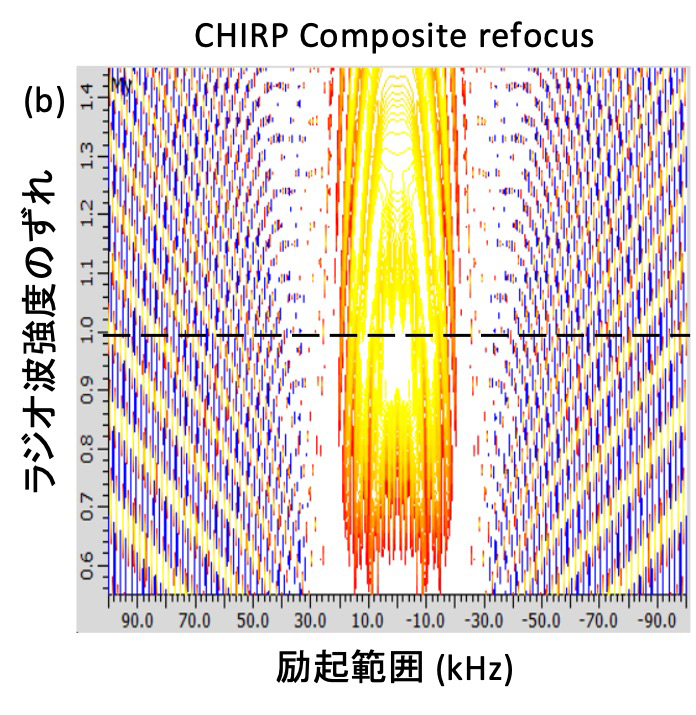
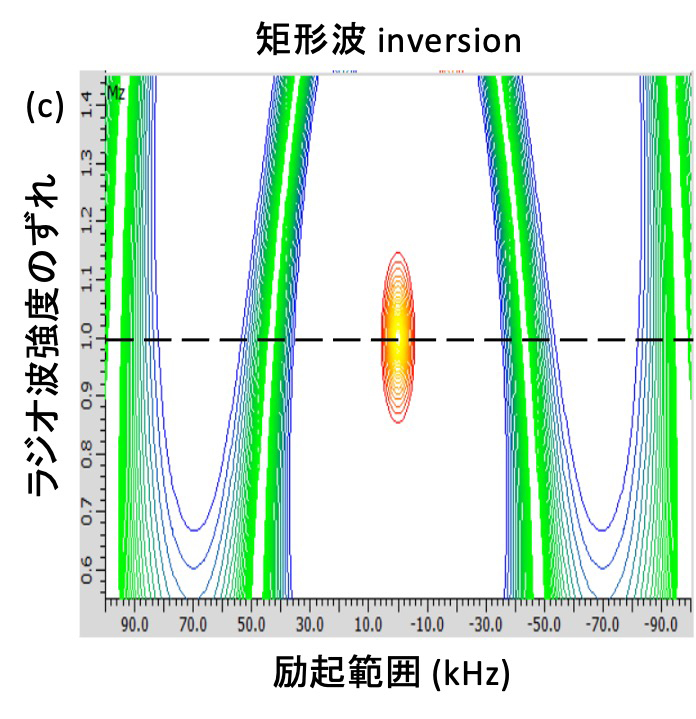
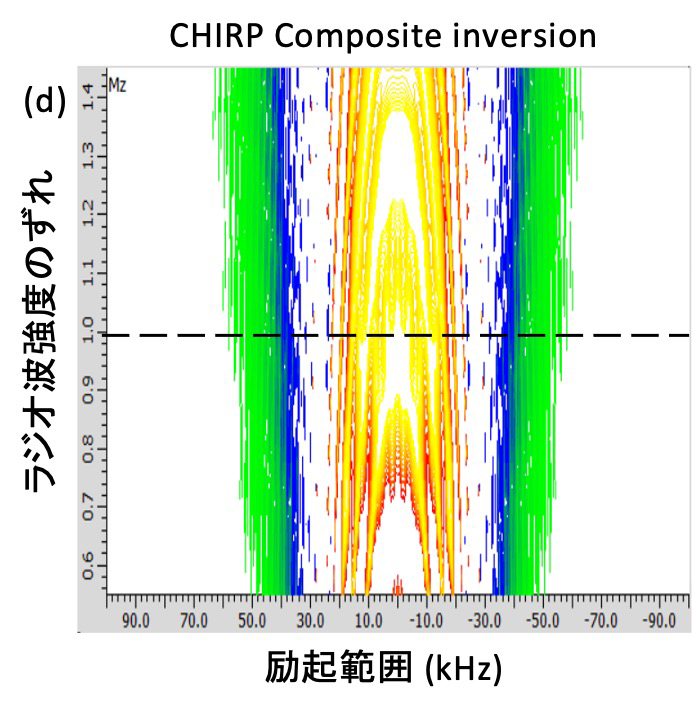
Figure 7 CHIRP Composite パルスの励起プロファイル
矩形波refocusパルス (a)、CHIRP Compositeパルスをrefocusとして用いた場合 (b)、矩形波inversionパルス (c)、CHIRP Compositeをinversionとして用いた場合 (d) の励起プロファイルを示す。CHIRP Compositeパルスはrefocusパルスとしてもinversionパルスとしても機能し、矩形波と比べて優れた励起プロファイルを持つ。

断熱パルスと緩和時間

断熱パルスは周波数を掃引することで励起を行っているため、励起している最中に緩和が起こると先に励起した部分の励起効率が後に励起した部分の励起効率より悪くなる場合がある。Fig. 6に緩和時間が0.9秒のサンプルおよび0.01秒のサンプルについて、2 ms のCHIRPパルスを用いた場合の実際の実験における励起プロファイルを示す。このように、緩和時間が短いサンプルに断熱パルスを用いた場合、緩和の寄与により励起効率に差が発生する可能性があるため注意が必要である。

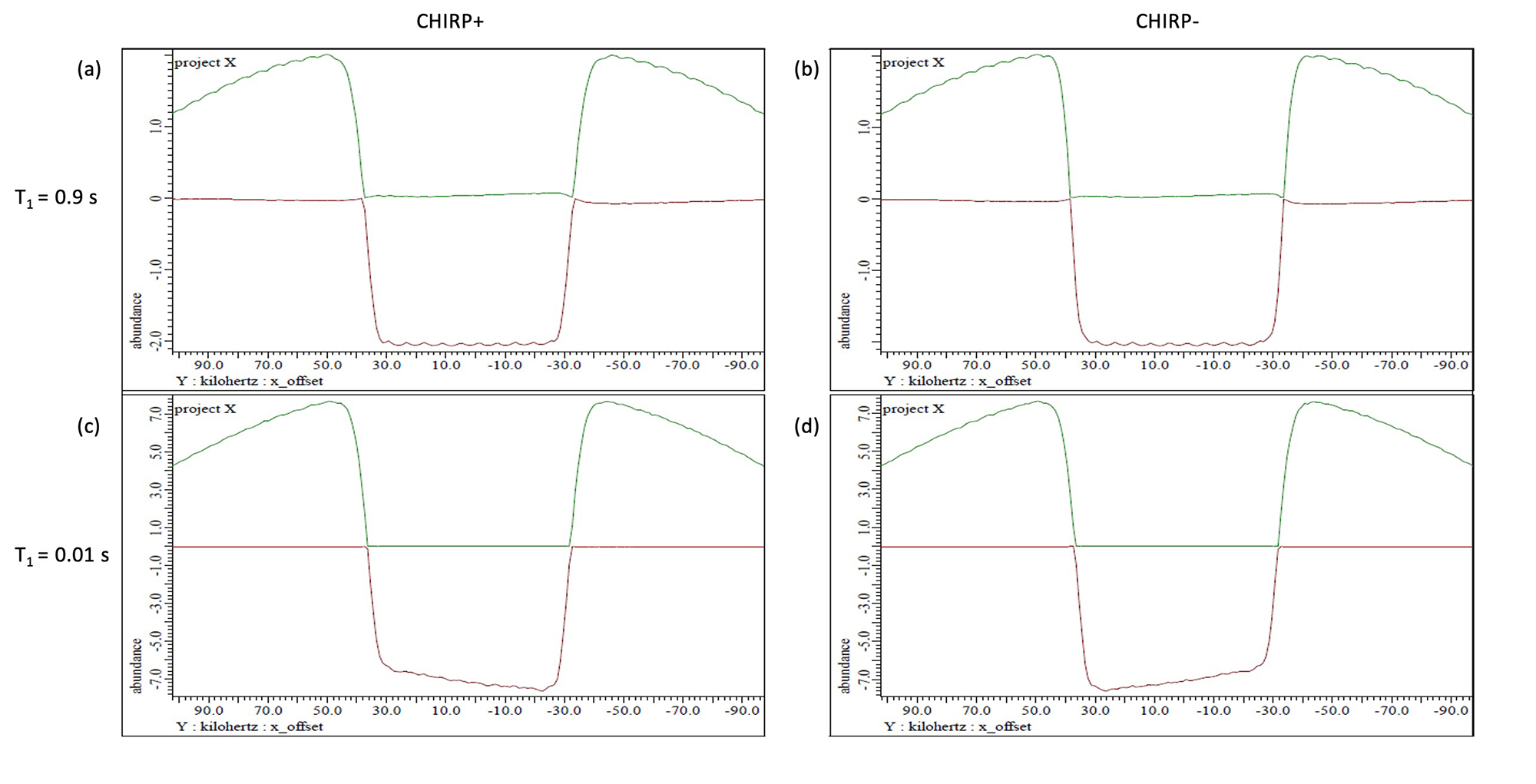
Figure 6 緩和時間の異なるサンプルでのCHIRPパルスの励起効率 T₁の異なるサンプルについて、CHIRP+ (周波数を上げていくCHIRP) あるいはCHIRP-(周波数を下げていくCHIRP) にて励起を行った際の励起プロファイルを示す((a) T₁ = 0.9 s, CHIRP+ (b) T₁ = 0.9 s, CHIRP- (c) T₁ = 0.01 s, CHIRP+ (d) T₁ = 0.01 s, CHIRP-) 。
サンプルにはH₂0 in D₂Oを用いて、offsetをずらして励起を行うことによって励起プロファイルを取得した。

まとめ

• 高磁場NMRにおいて、矩形波パルスは励起効率が不十分であり、しばしば広帯域パルスを用いる必要がある。

• ラジオ波の位相を変調することで、実質的に周波数を変調することが可能である。

• CHIRPパルスおよびWURSTパルスはinversionパルスとして機能する断熱パルスである。

• CHIRPパルスを3つ組み合わせたCHIRP Compositeパルスはinversionとrefocusの両方として機能する。

• 緩和時間の短いサンプルについては断熱パルスが適さない場合がある。

参考文献

Hwang, T. L., van Zijl, P. C. M., & Garwood, M. (1997). Broadband adiabatic refocusing without phase distortion. Journal of Magnetic Resonance (San Diego, Calif. : 1997), 124(1), 250–254. https://doi.org/10.1006/JMRE.1996.1049

Köck, M., Kerssebaum, R., & Bermel, W. (2003). A broadband ADEQUATE pulse sequence using chirp pulses. Magnetic Resonance in Chemistry, 41(1), 65–69. https://doi.org/10.1002/MRC.1097

Kupce, E., & Freeman, R. (1995). Stretched Adiabatic Pulses for Broadband Spin Inversion. Journal of Magnetic Resonance Series A (Vol. 117).

関連製品

核磁気共鳴装置 (NMR)