光と電子の強い相互作用(3)　＊＊＊　強磁性薄膜の『強結合』状態　＊＊＊

ER200008

マイクロ波光子とスピンの結合定数 𝑔_𝑚は、Application Note ER200007 の式(1)に示したように、スピン数（磁気モーメント）の平方根に比例する。そのため、スピン数の多い強磁性体で、特に線幅が細い試料を通常の方法でFMR測定すると、『Purcell effect』よりもさらに強い相互作用による『strong coupling （強結合）』の状態が達成され、正常なスペクトルが得られない。図1(a)は、そのような『強結合』状態になってしまったときの異常スペクトルの例である。図1(d)のように、充填率を大幅に下げ、『弱結合状態』にすると、図1(c)のように正常なスペクトルが得られる。

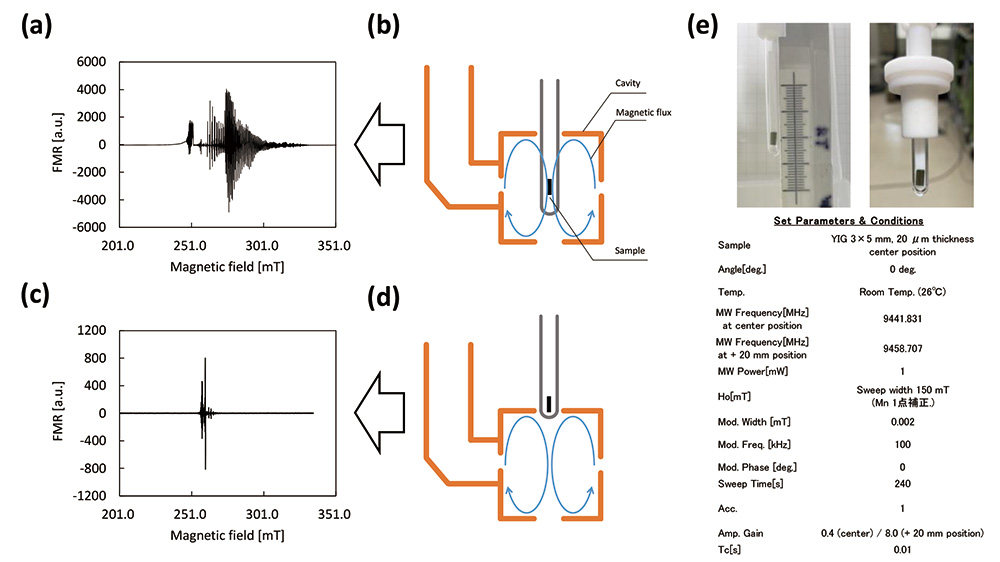
図1 強磁性薄膜試料（yttrium iron garnet（YIG））の強結合状態・弱結合状態のFMRスペクトル測定例

(a) 強結合状態によりESR装置からの異常信号を伴うYIG-FMRスペクトル。(b) (a)のスペクトルを測定したときの試料のキャビティ内配置。(c) 弱結合状態でのYIG-FMRスペクトル。(d) (c)のスペクトル測定したときの試料のキャビティ内配置。(e) YIG薄膜試料。

『強結合状態』におけるキャビティ周波数スペクトル

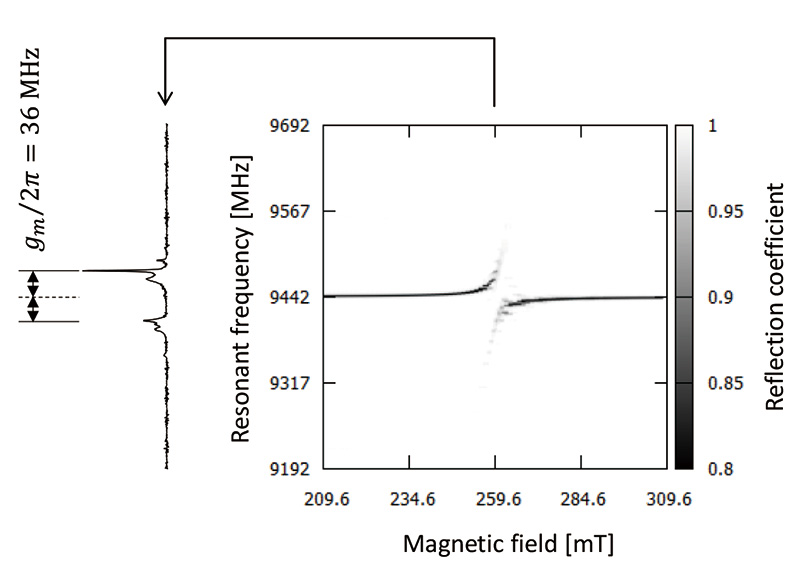
図2 YIG-CMPのキャビティ周波数スペクトルの例

図2は、上記試料をキャビティ中心にセットした状態で、キャビティの周波数スペクトル（Q-dip）を各磁場で測定した結果の二次元マップである。『Purcell effect』と違って、共鳴磁場に近づくと、スペクトルのピークが完全に分離して大きくシフトしていく。矢印で示した、共鳴磁場におけるスペクトル分裂幅から、結合定数 𝑔_𝑚∕ 2𝜋= 36 MHzと見積もることが出来る。Q_L値約8200 ( 𝑘_𝑐 ∕ 2𝜋 = 0.55 MHz) 、半値幅 (HWHM) 約75μT（ 𝛾_𝑚 / 2𝜋 = 2.1 MHz）より、𝑔_𝑚 > 𝑘_𝑐, 𝛾_𝑚なのでこの系は『強結合』状態にあると言える。このように、キャビティと強磁性体のマグノンが強結合状態にある系を『cavity-magnon polariton (CMP)』と呼ぶ。CMPは、マイクロ波の光子とマグノンのスピンが一体化して生成した『擬似粒子』とみなされる人工的な量子であり、近年、量子光学、量子情報物理等の分野で注目されている系である^[1]