JASON SMILEQによるNMR定量分析:精度向上への新手法
Part 2. 分散分析による要因の解析
NM250003
現在、JASON1 SMILEQ2では定量分析結果を基にした2種類の分析レポートを作成することが可能です。これらのレポートは、定量分析結果に基づいて測定の信頼性やデータ特性を深く解析するもので、包括的な情報を提供します。
このアプリケーションノートでは、「Part 1. 不確かさ要因の評価」の結果を基に分散分析へ展開し、誤差要因やその寄与をより具体的に分析した結果について解説します。さらに、Part 3では、Part 1およびPart 2で得られた結果を用いて、より詳細な不確かさ要因解析を行った結果について紹介します。
不確かさレポートから分散分析へ
不確かさレポートの偏差
不確かさレポートでは、各要素間の相互作用やデータ全体の変動の評価から拡張不確かさを算出します。これにより、測定プロセス全体の不確かさを統合的に解析するための重要な基盤が提供されます。
分散分析の役割
分散分析(ANOVA:Analysis of Variance)は、データに含まれる複数の要因が結果にどのように影響しているかを統計的に解析する手法です。この手法では、各要素の純粋な偏差を特定し、それぞれの要因の寄与度を明確にすることが可能です。また、要素間の影響を分離することで、誤差要因を詳細に分析するための土台を整える役割を果たします。
ANOVAレポートを通じた比較
ANOVAレポートの結果を活用することで、誤差要因や各要素の寄与率を具体的に分析できます。これにより、測定プロセスの改善に向けた明確な指針を得ることが可能です。この分析は、データの信頼性や精度を向上させるうえで欠かせないステップとなります。
分散分析: Two-way ANOVA の一般的な分析方法

Figure 1. Two-way ANOVAの模式図
Two-way ANOVA(2要因分散分析)は、2つの異なる要因(要因Aと要因B)がデータに及ぼす影響や、それらの相互作用を評価するための手法です。以下にその主要な計算要素を説明します。
要因A: 要因Aがデータに与える影響を解析します。
要因B: 要因Bがデータに与える影響を解析します。
相互作用(Interaction): 要因Aと要因Bが相互に影響を及ぼし、データに与える効果(要因A × 要因B)を解析します。
Error(誤差): 上記の要因や相互作用以外に起因するランダムなばらつきを指します。
総分散(Total Variance)は、これらすべての要素(要因A、要因B、相互作用、誤差)の寄与を統合して計算されます。Figure 1はTwo-way ANOVAの仕組みを模式図で示したものです。
JASON ANOVAの分析方法: 2 way ANOVA
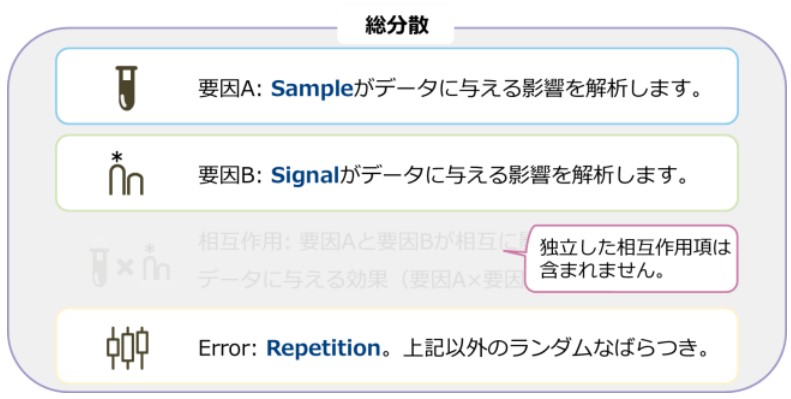
Figure 2. JASON 2 way ANOVAの模式図
JASON分散分析では、2つの異なる分析モデルを使用したレポートを提供します。JASON 2 way ANOVAは、独立した要因の影響に焦点を置き、データに影響を与える要素を個別に評価する簡潔な手法です。主に、以下の特徴を持ちます:
要因A(Sample): 背景要素として扱い、Signalとの直接的な関係性を考慮しません。Sampleの独立した寄与を評価します。
要因B(Signal): データに与える直接的な影響を解析します。Signalの独立した寄与を評価します。
相互作用: 独立した相互作用項は含まれません。
試料間の違いが小さい場合や、Signalそのものの効果が関心事項である場合に特に適しており、JASONのもう一つの分析モデルである2 nested way ANOVAよりも構造がシンプルで、個々の要因を解析する際に有用です。
Figure 2は、JASON 2 way ANOVAの仕組みを模式図で示したものです。
JASON ANOVAの分析方法: 2 nested way ANOVA
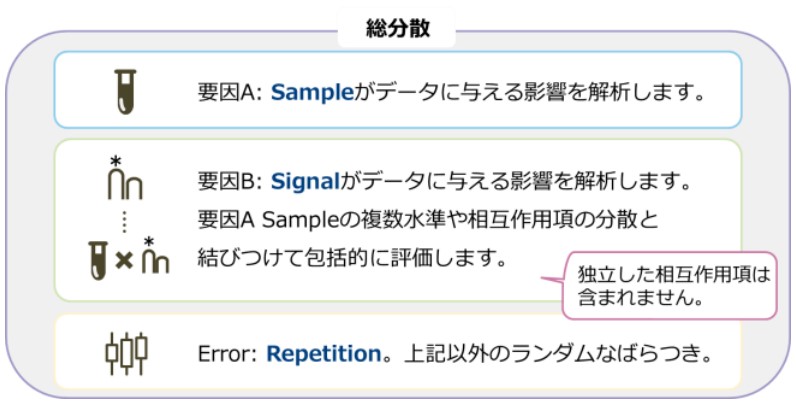
Figure 3. JASON 2 nested way ANOVAの模式図
JASON 2 nested way ANOVAは、複数の要因の関係性やその相互作用を評価する包括的な手法です。以下が主な特徴です:
要因A (Sample): 複数水準を通じて、データに影響を及ぼす要素を評価します。このモデルでも、2 way ANOVAと同様に背景要素として取り扱われます。
要因B (Signal): データに与える直接的な影響を解析します。Sampleの水準と関連付けて評価されます。
相互作用: 独立した相互作用項は含まれません。
Sampleの寄与が重要な場面や、Signalの効果をSampleとの相互作用を踏まえて解析する必要がある場合に適しています。複雑なデータ解析に対応し、より正確な結果を導きます。
Figure 3は、JASON 2 nested way ANOVAの仕組みを模式図で示したものです。またTable 1は、2つの分析モデルの違いについて比較した表です。
Table 1. 2 way ANOVAと2 nested way ANOVAの違い

ANOVAレポートの詳細
ANOVAレポートでは、それぞれの要因による変動量が Mean Square Variance(平均二乗分散) として算出されます。この平均二乗分散は分散分析を解釈する上で重要な指標であり、各要因の寄与度を量的に示します。得られた平均二乗分散を基に、各要因の偏差を計算することができます。この偏差は、特定の要因が他の要因や相互作用の影響を受けない状態で算出された変動量であり、「純粋な偏差(Pure Deviation)」と呼ばれます。この純粋な偏差を用いて、各要因ごとの影響を反映した不確かさを抽出することが可能です。このプロセスによって、データの精度や信頼性が定量的に評価され、解析結果をより深く理解するための基盤を構築することができます。Figure 4に、2 way ANOVAレポート結果に含まれる指標とそれぞれの説明を示します。
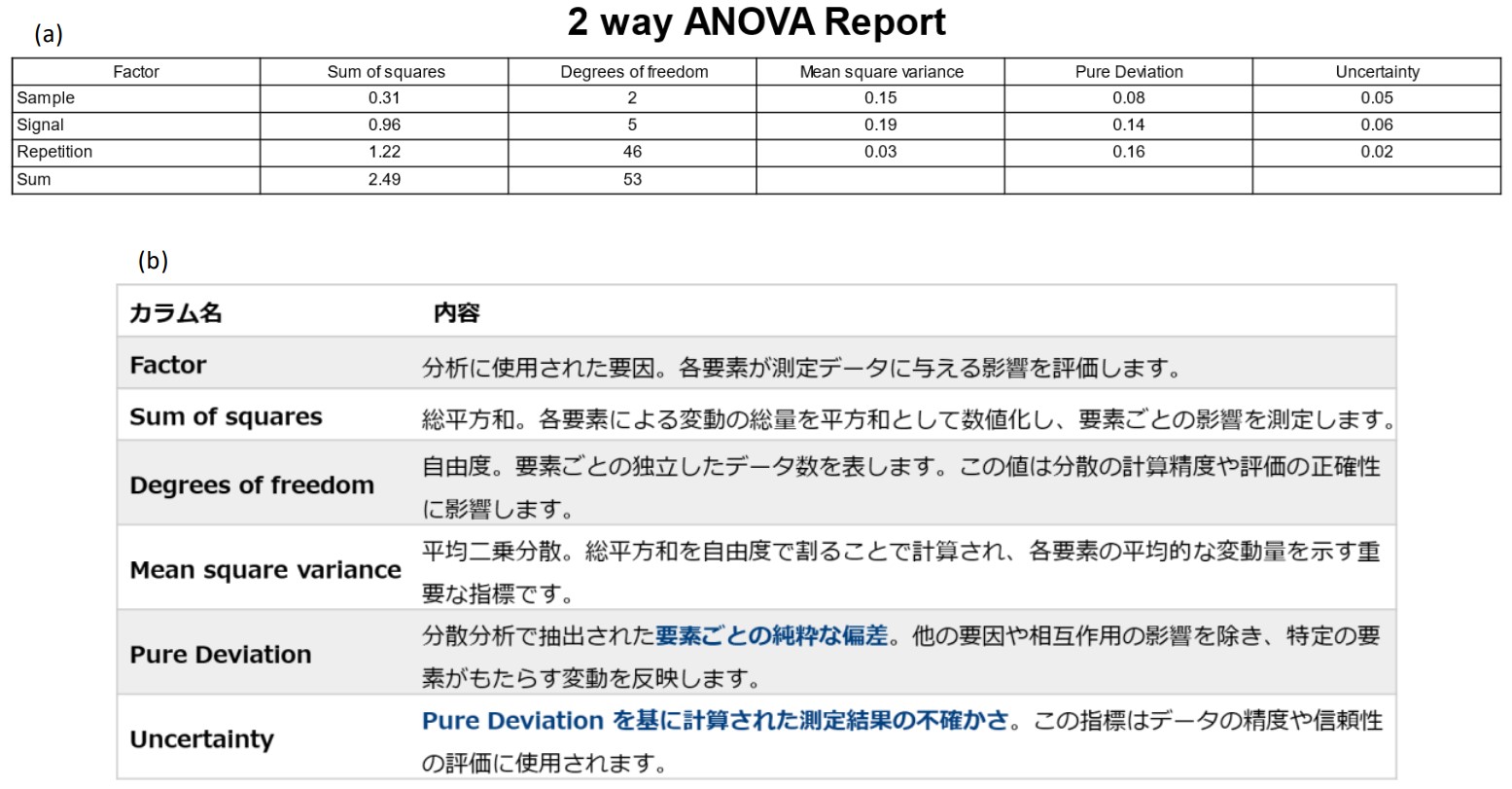
Figure4. ANOVAレポート: (a)ANOVAレポート結果例、(b)ANOVAレポート結果の指標とその説明
2 way ANOVA と不確かさレポート結果の比較
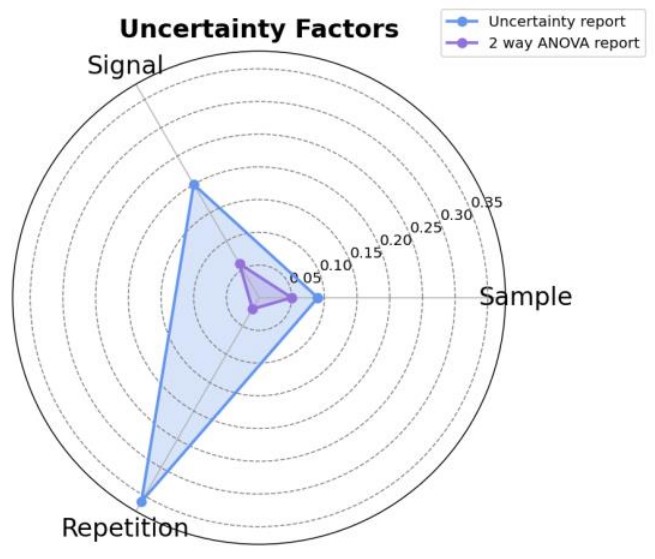
Figure 5. 2 way ANOVAと不確かさレポートの比較結果
Figure 5は、2 way ANOVAの結果と不確かさレポートの結果(アプリケーションノート NM250002)をレーダーチャートで比較しています。紫色は2 way ANOVAの結果、青色は不確かさレポートの結果を示しています。以下の傾向が確認されます:
Sample: 不確かさレポートの値よりも低く、純粋な影響のみが抽出されていることがわかります。
Signal: 値が小さく、他の要因や相互作用の影響が軽減されていることが明確です。
Repetition: 非常に小さい値を示しており、測定プロセス自体の安定性が高いことを示しています。
不確かさレポートの結果との差について
2つのレポートによる結果の差は、Table 2に示された特徴から説明できます。不確かさレポートが「最悪のケースを考慮した評価」を提供し、繰り返し誤差が相対的に大きく評価される傾向にあるのに対して、分散分析は「データ特性の全体像を反映した評価」を行う手法であり、他の要因から分離した不確かさが抽出されています。さらに分散分析を活用することで、要因ごとの詳細な分析が可能となります。
Table 2. 不確かさレポートとANOVAレポート結果の特徴

不確かさレポート結果との差の考察
不確かさレポート結果との差を分析するにあたり、以下の手順で分散分析結果を検討します。まず、分散分析結果の妥当性を確認し、次に2つの分散分析モデルの結果を用いて要因の解析を行います。
データの統計性の確認: 前提となるデータの統計的性質を評価し、不確かさと分散分析結果の妥当性を確認します。この解析では、レポートデータを用いてPythonで計算を行いました。評価手法には以下を使用します:
- IQRテスト
- Shapiro-Wilkテスト
- QQプロット
- KDEプロット
分散分析の要因評価: データのばらつきや不確かさが各要因にどのように寄与しているかを確認します。この過程では、2 way ANOVAおよび2 nested way ANOVAの結果を比較し、要因ごとの相対的な影響を整理します。
1. データの統計性の確認: 外れ値検証(IQRテスト)
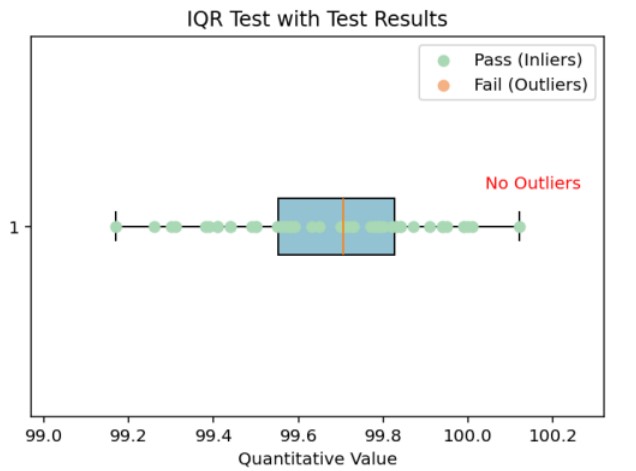
Figure 6. IQRテスト結果
IQRテスト(四分位範囲法)は、データの外れ値を検出するための手法の一つです。IQRは、第3四分位数(Q3)から第1四分位数(Q1)を引いた値で定義され、データの中央50%の範囲とともに算出されます。Figure 6に示された箱ひげ図では以下を表しています:
箱(IQR): Q1からQ3の範囲。
箱の中の線: データの中央値(50%地点)。
Whiskers: データ全体の範囲。
この分析の結果、外れ値は検出されず、データのばらつきが小さいことが確認されました。
1. データの統計性の確認: 正規性の確認
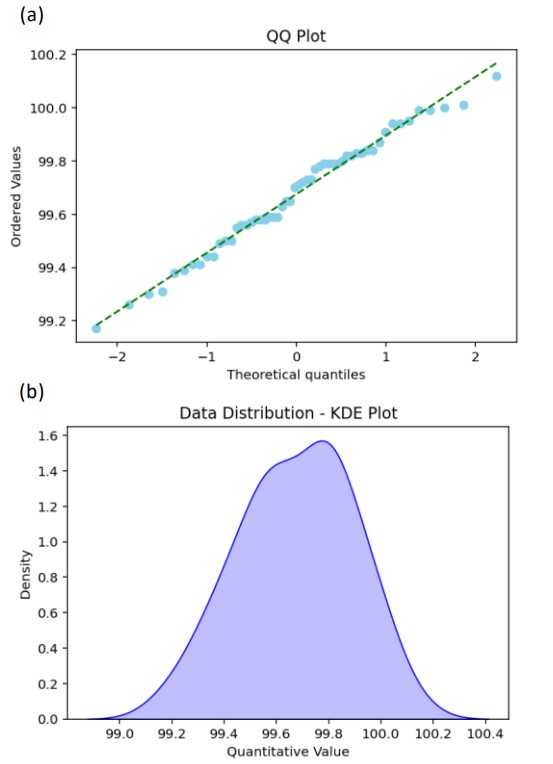
Figure 7. データの統計性の確認: (a)QQプロット、(b)KDEプロット
Shapiro-Wilkテスト
Shapiro-Wilkテストは、データの正規性を検定するための統計的手法です。このテストでは、帰無仮説として「データが正規分布に従う」を設定します。算出されたp値: 0.6092は0.05より十分に大きいため、データが正規分布であることが確認されました。
QQプロット (Quantile-Quantile Plot)
QQプロットは、データの分布を理論的な正規分布と比較するためのプロットです。プロット上で理論値(正規分布)と実データの点が直線上に近いほど、正規性が高いことを示します。Figure 7(a)は、計算結果を用いて作成されたQQプロットを示しています。このプロットより、統計的にデータの正規性が確認されました。
KDEプロット (Kernel Density Estimate)
KDEプロットは、データの分布を滑らかに表現する方法で、ヒストグラムよりも正確にデータ密度を表示できます。 Figure 7(b)は、計算結果を用いて作成されたKEKプロットを示しています。このプロットより、データの正規性が視覚的にも確認されました。
分散分析の妥当性の評価
以上の手法による検証結果から、分散分析の妥当性が確認されました。正規性が統計的・視覚的に評価されており、信頼性の高い解析結果が得られる基盤が整っていることがわかります。
2. 分散分析の要因評価
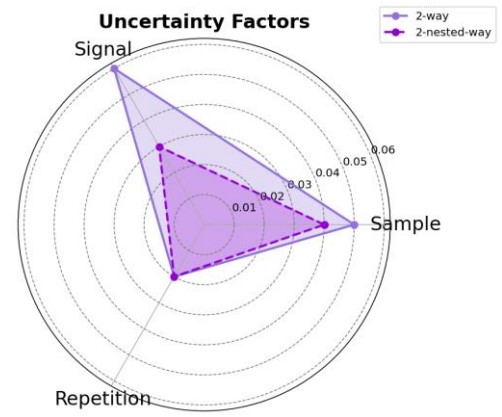
Figure 8. JASON ANOVA 分析結果
Figure 8は、2 way ANOVAと2 nested way ANOVAの結果をレーダーチャートで比較した図です。紫色が2 way ANOVAの結果、濃い紫色が2 nested way ANOVAの結果を示しています。以下のような傾向が確認されます:
Sample: 2つのモデルで近似した値を示しており、ばらつきの安定性が確認されます。ただし、2 way ANOVAでは他の要因との相互作用が影響している可能性が示唆されます。
Signal: 2 nested way ANOVAでは値が低く、2 way ANOVAでは相対的に高い値が得られました。この結果は、Signalが繰り返し誤差やSample、標準試料との相互作用に対して敏感である可能性を示しています。
Repetition: 繰り返し誤差の値は両モデルでほぼ同程度を示し(0.02)、非常に安定していることが確認されました。また、測定データ全体のばらつきが最小限に抑えられている点も明らかになりました。
分散分析結果のまとめ
不確かさレポートとの比較を踏まえ、分散分析から以下の内容が確認されました:
分散分析の妥当性: 各要因の不確かさが統計的に妥当であることが確認され、定量分析結果における影響が明確化されました。
繰り返し誤差: 繰り返し誤差は極めて小さい値を示しており、測定プロセスの安定性とデータの信頼性が裏付けられました。
標準試料の影響: 標準試料の不確かさが測定全体に波及しており、主要な影響要因であることが判明しました。
相互作用の影響: SignalとSampleの相互作用が測定データの不確かさに寄与する可能性が示唆されました。
これらの結果は、定量分析の信頼性向上に向けた重要な知見を提供しています。
標準試料の不確かさが定量分析結果に与える影響とは?
これまでの解析結果から、測定システム全体の繰り返し誤差は非常に小さいことが確認され、測定プロセスの安定性が示されました。一方で、標準試料による不確かさが測定結果にどのような影響を及ぼしているかについては、さらに詳しい検討の余地があります。
この課題の解明には、シミュレーションなどの方法を活用した詳細な分析が有効です。特に、標準試料の特性がデータ全体に波及する影響を評価することで、測定の精度や信頼性を向上させる鍵が得られると考えられます。本解析の詳細については、「Part 3. シミュレーション分析による要因の解明」にてさらに掘り下げて解説します。
[1] JEOL Analytical Software Network
[2] Spectral Management Interface Launching Engine for Q-NMR
分野別ソリューション
関連製品
関連情報
アプリケーションノート「JASON NMRソフトウェアのSMILEQアドオンによる自動1H定量NMRシステム NM220008」


