ζ因子法
ζ因子法
zeta factor method, ζ factor method
[目次:分光分析(EELS/EDS/電子構造)]
TEMにおける薄膜試料のEDS分析において、元素の定量に用いる手法の一つ[1]。広く用いられているクリフ・ロリマー法 (Cliff-Lorimer法)を改善し、試料の密度と厚さが未知の場合でも高い精度の定量分析ができるのが特徴である。
特性X線強度からの組成の決定
ζ因子法 (ζファクター法)では、測定した特性X線強度に ζi 因子と呼ばれる係数を掛けることで、元素の組成を、次式を用いて決定する。
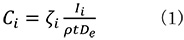
Ci: 元素iの組成
Ii: 元素iの特性X線強度
ρt:質量膜厚
De: 照射電子量 (De = 電子電荷×照射電流量×測定時間)
(1)式で用いられる ζi とρt の求め方を以下に示す。
ζ因子(ζファクター)の決定
元素iのζ因子 (ζi)は、イオン化断面積Qi 、蛍光収率ωi (特性X線の発生確率)や照射電子量De 等から以下のように定義される。
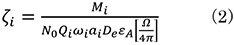
M: 原子量
N0: アボガドロ定数
Qi: 元素iからの特性X線のイオン化断面積
ωi: 元素iからの特性X線の蛍光収率
ai: 元素iからの全てのK (L, M) 線に対するKα (Lα,Mα) 線の比
De: 照射電子量 (De = 電子電荷 × 照射電流量 × 測定時間)
εi : 元素iからの特性X線の検出効率
Ω: 検出立体角
ζ因子は式 (2)から理論的に決定することが可能である。しかし、計算に用いるイオン化断面積を求めるためのモデルの取り方によってQi の値が変わり、ζ因子の値に任意性が出ることがある。そのため、目的の元素を含み、組成および膜厚が既知の薄膜標準試料からζ因子を実験的に決定することが多い。
質量膜厚(ρt)の決定
ζファクター法では、測定した特性X線の強度から以下のように質量膜厚 (ρt)を見積もることができる。
すべての元素について組成の総和を取ると、∑i Ci =1が成り立つので、式(1)は次の式のようになる。
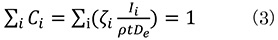
式 (3)を変形して、質量膜厚 ρt は次式から求めることができる。
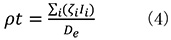
ζファクター法では、ζ因子を式 (2)または実験的に求め、さらに式 (3)から質量膜厚を決定することによって、試料の密度と厚さが未知の場合でも、特性X線強度を測定するだけで組成を決定できる。本手法は、試料中での吸収を無視できないエネルギー領域の特性X線 (軟X線)においても、高い精度の定量分析ができる。
なお、EDSによる薄膜試料の定量分析で一般的に用いられるクリフ・ロリマー法 (Cliff-Lorimer法)では、試料の密度と厚さが既知でないと、特性X線の吸収効果を補正できない。そのため、試料の密度と厚さが未知の場合、吸収効果の補正が不正確になるため、吸収の影響が無視できない特性X線を含む試料では定量精度が良くない。
[1] M. Watanabe and D.B. Williams: "The Quantitative Analysis of Thin Specimens: a Review of Progress from the Cliff-Lorimer to the New ζ-Factor Methods", J. Microsc. 221 (2006), 89-109.
(Lehigh大学 渡辺 万三志教授による)
A quantitative elemental analysis method using energy-dispersive X-ray spectroscopy (EDS) in a TEM [1]. The ζ (zeta) factor method improves the Cliff-Lorimer method which has widely been used for EDS quantitative analysis. The main advantage of the ζ factor method exists in high-accuracy quantitative analysis even when the density and thickness of a specimen are unknown.
Chemical (elemental) composition determination using the characteristic X-ray
In the ζ (zeta) factor method, the chemical (elemental) composition of the specimen is determined by multiplying the factor ζi to the measured characteristic X-ray intensity Ii using the following equation.
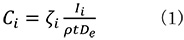
Ci: Chemical composition of Element i
Ii: Characteristic X-ray intensity of Element i
ρt:Mass thickness
De: Electron illumination dose (De = Electron charge Χ Illumination current Χ Measurement time)
The methods of obtaining ζi and ρt used in the equation (1) are described in the following way.
Determination of the ζ (zeta) factor
The ζ (zeta) factor (ζi) of element i is defined by using ionization cross section Qi, fluorescence yield ωi (characteristic X-ray generation probability) and electron illumination dose De.
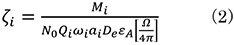
M: Atomic weight
N0: Avogadro constant
Qi: Ionization cross section of the characteristic X-ray from Element i
ωi: Fluorescence yield of the characteristic X-ray from Element i
ai: Ratio of Kα (Lα or Mα) lines to all of K (L or M) lines from Element i
De: Electron illumination dose (De = Electron charge Χ Illumination current Χ Measurement time)
εi : Detection efficiency of the characteristic X-ray from Element i
Ω: Detection solid angle
The ζ (zeta) factor can be determined theoretically by the equation (2). However, since the value of Qi is dependent on the model to obtain the ionization cross-section, the value of ζ factor is somewhat arbitrary. Thus, in many cases, the ζ factor is experimentally determined using a thin film standard specimen, which contains the target element and has a known composition and thickness.
Determination of mass thickness (ρt)
In the ζ (zeta) factor method, the mass thickness (ρt) of the specimen can be estimated using the measured characteristic X-ray intensity as expressed below.
Taking the sum for the compositions of all constituent elements, ∑i Ci =1. Then, the equation (1) is expressed as follows.
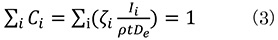
From equation (3), the mass thickness (ρt) is obtained by the next equation.
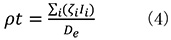
Therefore, the ζ (zeta) factor method offers determination of the chemical (elemental) composition of the specimen from the measured characteristic X-ray intensity using the ζ factor obtained through the equation (2) or experimentally, with the mass thickness obtained by the equation (3), even when the density and thickness of the specimen are unknown. It should be noted that the method enables high-accuracy quantitative analysis even for the characteristic X-rays with low energies (soft X-rays) where the absorption effect in the specimen is negligible.
The Cliff-Lorimer method is used commonly for the EDS quantitative analysis. However, by this method, proper correction of the absorption effect of characteristic X-rays can be performed only when the density and thickness of a specimen are known. Thus, the accuracy of the quantitative analysis of EDS is not sufficient for the characteristic X-rays, which suffers the absorption effect as far as the density and thickness of the specimen are unknown.
[1] M. Watanabe and D.B. Williams: "The Quantitative Analysis of Thin Specimens: a Review of Progress from the Cliff-Lorimer to the New ζ-Factor Methods", J. Microsc. 221 (2006), 89-109.
(By Professor Masashi Watanabe, Lehigh University)
関連用語から探す
説明に「ζ因子法」が含まれている用語






