ローゼンタール-ヘンダーソンB因子

Rosenthal-Henderson B-factor

Rosenthal-Henderson B-factor (RH-B因子) は、デバイワラー因子とは異なり原子の熱振動のみならず、試料ドリフト、氷の厚さ、検出器の空間周波数特性、電子ビームの干渉性、その他測定と像解析に伴う誤差のすべてを考慮した、構造因子に対する減衰因子である。このRH-B因子は単粒子解析において、三次元再構成した結果の分解能と、その分解能を得るのに必要な粒子像の数を関係づける係数になっている。目標とする分解能を得るために必要な粒子像の数を見積もるために導入されたものである。

図1を用いてアポフェリチン粒子の単粒子解析におけるRH-B因子の事例を示す。図はアポフェリチン粒子の数Nの自然対数 (ln N) に対して、N個の粒子像による単粒子解析で得られた分解能に対応する空間周波数k₁ (フーリエシェルコリレーションが0.143となるk) の二乗 (k₁²) を示している。このグラフをRosenthal-Henderson plotと呼び、プロットが描く直線の傾きの二倍がRH-B因子である。アポフェリチンのように安定な構造をとる場合は、RH-B因子が50程度であれば十分良い分解能が得られることが知られている。この事例では最終的に33万個の粒子を用いた解析でd＝1/ｋ₁＝1.53Åの分解能が得られており、RH-B因子の値は51であった。

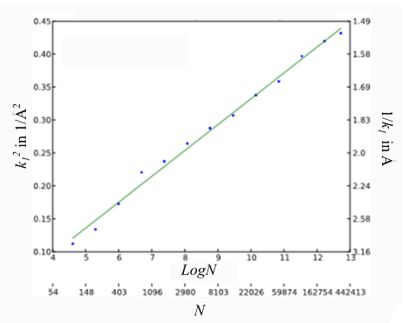
図1 Rosenthal-Henderson plotの一例を示す。

青色の点は、撮影されたアポフェリチン粒子の数Nの自然対数ln Nに対してフーリエシェルコリレーションが0.143となる空間周波数k₁の二乗k₁²を示す。緑色の直線は、青色の点に対する線形フィッティングで、その傾きの2倍からRH-B因子の値は51と算出される。

RosenthalとHendersonは、2003年の論文 [1] において、Rosenthal-Henderson B-factorを導入した。
原子による量子線 (X線、中性子線、電子線) の散乱振幅fは原子の熱振動によって減衰する。原子の熱振動による減衰を表す量として導入されたデバイワラー因子 (Bファクターまたは温度因子とも言う) は、次式で与えられる。

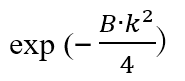
ここで、Bは、原子の熱振動の振幅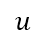の平均二乗振幅 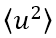(atomic displacement parameter (ADPともいう)を用いて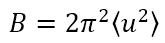と書け、通常Å²の単位で表される。散乱波の波数kは、 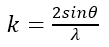(λ: 量子線の波長、θ:散乱角の1/2) である。この結果、原子散乱因子は波数の増加に伴って減衰し、次式で与えられる。

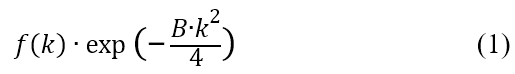
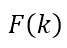をタンパク質粒子の構造因子とする。構造因子の空間周波数 kに対する減衰を、式 (1) の類推から次のように表す。

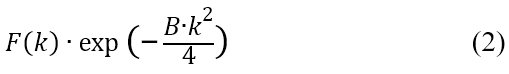
一枚の分子像の周波数kでのノイズの振幅を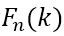周波数kのノイズの振幅とすると (nはノイズを意味する)、N個の粒子像について平均したノイズの振幅は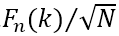となる。式(2)がノイズの振幅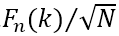と等しくなる周波数を到達空間分解能（の逆数）と定義すると、そのときの空間周波数k₁は

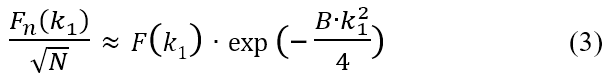
で与えられる。両辺の自然対数をとると次式を得る。

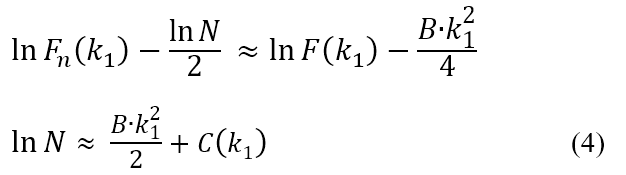
ここで、

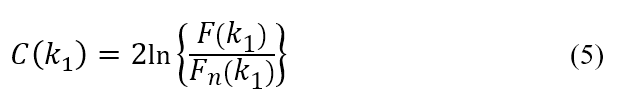
到達分解能付近で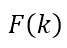周波数kのノイズの振幅は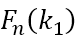と近い値を取ると考えられるため、式(4)の 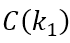C(K1)小さな定数は小さな定数となる。

式 (4) で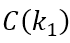 C(K1) を無視して、蛋白質粒子像の数Nの対数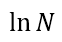を横軸に、k₁²を縦軸にプロットすると直線になり、その傾きがB/2であることがわかる。（したがって、蛋白質粒子の構造因子を具体的に計算する必要はない。）

(監修: 米倉功治理化学研究所放射光科学研究センターグループディレクター、東北大学多元物質科学研究所教授)

参考文献 Reference

[1] Rosenthal, PB, Henderson, R., J. Mol. Biol. 333, 721–745 (2003)

The Rosenthal-Henderson B-factor (RH B-factor) is a damping factor for the structure factor used in the case of Single Particle Analysis (SPA). The RH B-factor is different from the ordinary Debye-Waller factor dealing with only the effect of atom vibrations (see “Related Terms”). The RH B-factor factor takes account of not only thermal vibrations of atoms, but also specimen drift, the thickness of ice, the spatial frequency response of the detector, the coherence of an electron beam, and the errors arising from measurement and image analysis. The RH B-factor is a coefficient that relates the spatial resolution obtained from the 3D reconstruction analysis in SPA to the number of particle images required to achieve that resolution. The RH B-factor was introduced to estimate the number of the particle images required to achieve a sufficiently high resolution in SPA.

Fig. 1 illustrates an example of the RH B-factor in SPA for apoferritin particles. The figure plots the square (k₁²) of the spatial frequency k₁ ("k₁" is the spatial frequency for the value of Fourier Shell Correlation (FSC) = 0.143), which corresponds to the spatial resolution obtained in SPA using the number of N particle images, against the natural logarithm (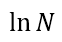) of the number of N apoferritin particle images. This graph is called "Rosenthal-Henderson plot". The RH B-factor is equal to twice the slope of a straight line drawn on the graph. In the case of stable-structure particles like apoferritin particles, it is known that a sufficiently high resolution is achieved for an RH B-factor of approximately 50. In this example, a spatial resolution of d＝1/ｋ₁＝1.53 Å was attained from the analysis using 330,000 particle images at a value of the RH B-factor of 51.

Fig. 1. Example of Rosenthal-Henderson plot.

Blue points, the square (k₁²) of the spatial frequency k₁ for a value of Fourier Shell Correlation (FSC) = 0.143 are plotted against the natural logarithm (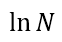) of the number N of apoferritin particle images. A green straight line shows a linear fitting for the blue points. The value of the RH B-factor is calculated to be 51 from twice the slope of the green line.

In 2003, Rosenthal and Henderson proposed the RH B-factor for SPA [1].
The scattering amplitude f of quantum rays (X-rays, neutrons and electrons) by atoms is damped by the thermal vibrations of the atoms. The Debye-Waller factor (temperature factor), introduced as a quantity to describe the damping of the scattering amplitude due to thermal vibrations of the atoms, is given by

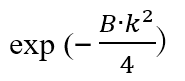
Here, B is written as 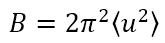and expressed in units of Å², where 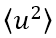(called atomic displacement parameter (ADP)) is the mean square amplitude u for thermal vibrations of an atom. The wave number k of the scattering wave is defined as 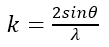(λ: the wavelength of the quantum wave, θ: half angle of the scattering angle). Then, the atomic scattering factor is attenuated with increasing the wave number and given by

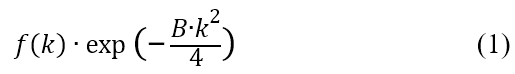
Let "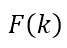" be the structure factor of a protein particle. The structure factor attenuates with increasing the spatial frequency k, and is expressed as follows analogous to the equation (1),

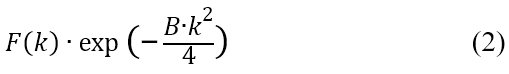
If the amplitude of the noise at a frequency k from a single protein particle image is 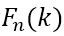, (n means noise), the amplitude averaged over the N particle images is 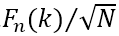. Then, we assume that the frequency k₁ at which equation (2) is equal to the amplitude of the averaged noise 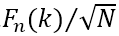, is the reciprocal of the spatial resolution attained. The spatial frequency k₁is given by

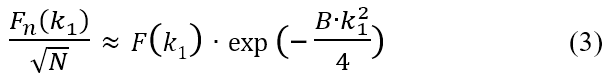
By taking the natural logarithm of both sides of equation (3), the following equations are derived.

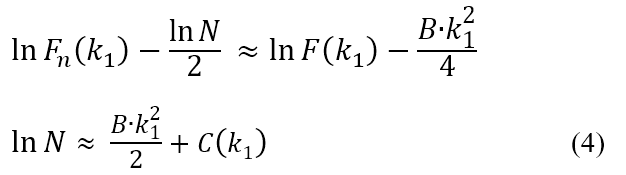
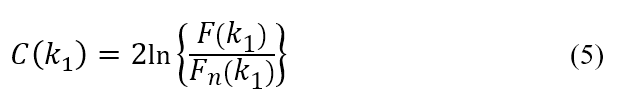
Since 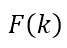is considered to take a value close to 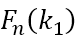near the attained resolution, 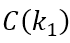in the equation (4) is to be a small constant.
Neglecting 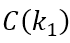in equation (4), plotting 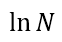(the natural logarithm of the number of N protein particle images) on the horizontal axis and k₁² on the vertical axis provides a straight line with a slope of B/2. (Thus, it is not needed to calculate the structure factor of the protein particle.)

(Confirmed by Professor Koji Yonekura, Tohoku University, RIKEN Spring-8 Center)