エワルド球

Ewald sphere

ある逆格子点から、試料結晶に対する入射波の方向に沿って入射波の波長の逆数１/λの距離にある点を中心として画いた、半径１/λの球のこと。エワルド球は、どのブラッグ反射が起るかを、逆空間における入射波ベクトルと逆格子点の関係を使って説明するのに用いられる。エワルド球の上に乗っている逆格子点は全てブラッグ条件を満たす。入射波が高速電子(100～200keV)の場合、エワルド球の半径は逆格子点の間隔に比べて非常に大きくなり、エワルド球を平面と近似できるので、エワルド球と逆格子点との断面として現れる反射の指数付けはX線回折の場合に比べて容易にできる。

Ewald sphere⇒図
金(Au)の[001]入射での逆格子点列 (格子面間隔d=0.204nm) とエワルド球。小さい円はMoKα特性Ｘ線 (λ=0.07109nm)、大きい円（円弧）は加速電圧200kVの電子線 (λ=0.002508nm) に対するエワルド球である。電子顕微鏡の取込角の一般的な限界である±10°まで表示してある。青色の逆格子点はブラッグ条件を近似的に満たす。

The Ewald sphere is a sphere of the radius defined as the reciprocal of the wavelength of the incident wave 1/λ, and is drawn with the point as the center, the point being at the length 1/λ from a certain reciprocal lattice point along the direction of the incident wave to a specimen crystal. The Ewald sphere explains what Bragg reflections occur using the relation between the incident wave vector and the reciprocal lattice points. All of the reciprocal lattice points on the Ewald sphere satisfy the Bragg condition. For a high energy incident electron (100 or 200 keV), the Ewald sphere can be approximated as a flat plane because the radius of the Ewald sphere is much larger than the distance between the reciprocal lattice points. As a result, the reflections, which appear as cross sections between the Ewald sphere and the reciprocal lattice points, can be indexed easier than the indexing in X-ray diffraction.

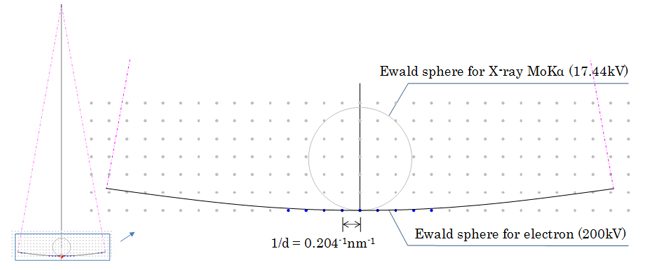
The reciprocal lattice points of gold (Au) for [001] incidence (lattice spacing d = 0.204 nm) and the Ewald spheres. The small sphere is the Ewald sphere for X-ray of MoKa (λ = 0.07109 nm) and the large sphere (arc) is the Ewald sphere for an electron beam of 200 kV (λ = 0.002508 nm).
The Ewald sphere for the electron beam is displayed up to ±10°, which corresponds to a usual limitation of the acceptance angle of an electron microscope. Blue reciprocal lattice points approximately satisfy the Bragg condition.