逆格子

reciprocal lattice

[目次：理論(電子の散乱／回折／結像)]

実格子の各格子面（結晶格子面）に垂直で、実格子の面間隔の逆数の距離で作られる点（逆格子点）の集まり。実格子が与えられれば逆格子は一義的に導かれる。

逆格子の基本単位ベクトルa*, b*, c* は、実格子の基本単位ベクトルa, b, cを使って、次式のように定義される(作られる)。

これらの式の分母は実格子の単位胞の体積Vに等しい。すなわち、

V=a∙(b×c)=b∙(c×a)=c∙(a×b).(2)

したがって、a*, b*, c* は次のように書ける。

a* は実格子のbとcで作られる面に垂直であることが分かる。同様にして b*はcとaで作られる面に垂直で、c*は aとbで作られる面に垂直である。

逆格子はa*, b*, c* の一次結合によって作られる。逆格子ベクトルgはh,k,l を整数として次のように書ける。

g = ha*＋kb*＋lc*.(4)

逆格子ベクトルgは実空間での結晶格子面（h k l）（ミラー指数という）に垂直である。ベクトルgの大きさ(長さ)は格子面（h k l）の面間隔dの逆数になっている｜g｜＝1/d。実格子の基本単位ベクトルa, b, cの次元は[r]¹であるのに対してa*, b*, c*の次元は[r]^-1なので、a*, b*, c*で作られる格子は逆格子と呼ばれる。

逆格子を使う利点は、実空間での結晶の格子面が逆格子空間では逆格子点として（面を点として）扱えるからである。逆格子空間でのエワルドの作図を用いると、どの格子面が反射条件（ブラッグ条件）を満たしているかを簡単に見つけることができる。エワルドの作図は次のようにして行う。
図の中の点は逆格子点を表す。逆格子点の一つを選んで、その逆格子点から電子線の入射方向と反平行に距離1/λ（＝|ｋ₀|）遡った地点を原点とする。原点から今選んだ逆格子点に向かって引いた線が電子線の入射ベクトルｋ₀になる。原点を中心として半径1/λの球を描く（図では2次元の円になっている）。この球をエワルド球という。エワルド球の球面上に乗っている全ての逆格子点gがブラッグの反射条件を満たしている。原点から逆格子点gに向かうベクトルｋは反射線のベクトルになる。図から、反射条件として次の式が得られる。

ｋ-ｋ₀ = g(5)

これをラウエ条件という。入射線ｋ₀は格子面（h k l）で反射されベクトルgだけ方向を変えてｋ= ｋ₀＋gとなって結晶から飛び去る。

ｋ₀とｋのなす角を2θとすると、ｋ-ｋ₀の大きさは ( $\frac{1}{\lambda }$ )×2sinθ となる。ｇの大きさは1/dだったので、式(5)は

となる。これを整理すると、

2dsinθ=λ(7)

となってブラッグの式が得られる。すなわち、エワルドの作図から導かれたラウエ条件はブラッグ条件と同じものであることが分かる。

ブラッグ条件は、結晶による回折を実空間のスカラー量で記述したものであり、直感的で理解しやすい。他方、ラウエ条件は回折現象を逆空間のベクトル量で記述したものである。ラウエ条件は抽象的であるが、回折現象を理論的に扱うのに適しており、回折現象のさらに進んだ取り扱いには欠かせない記述法である。

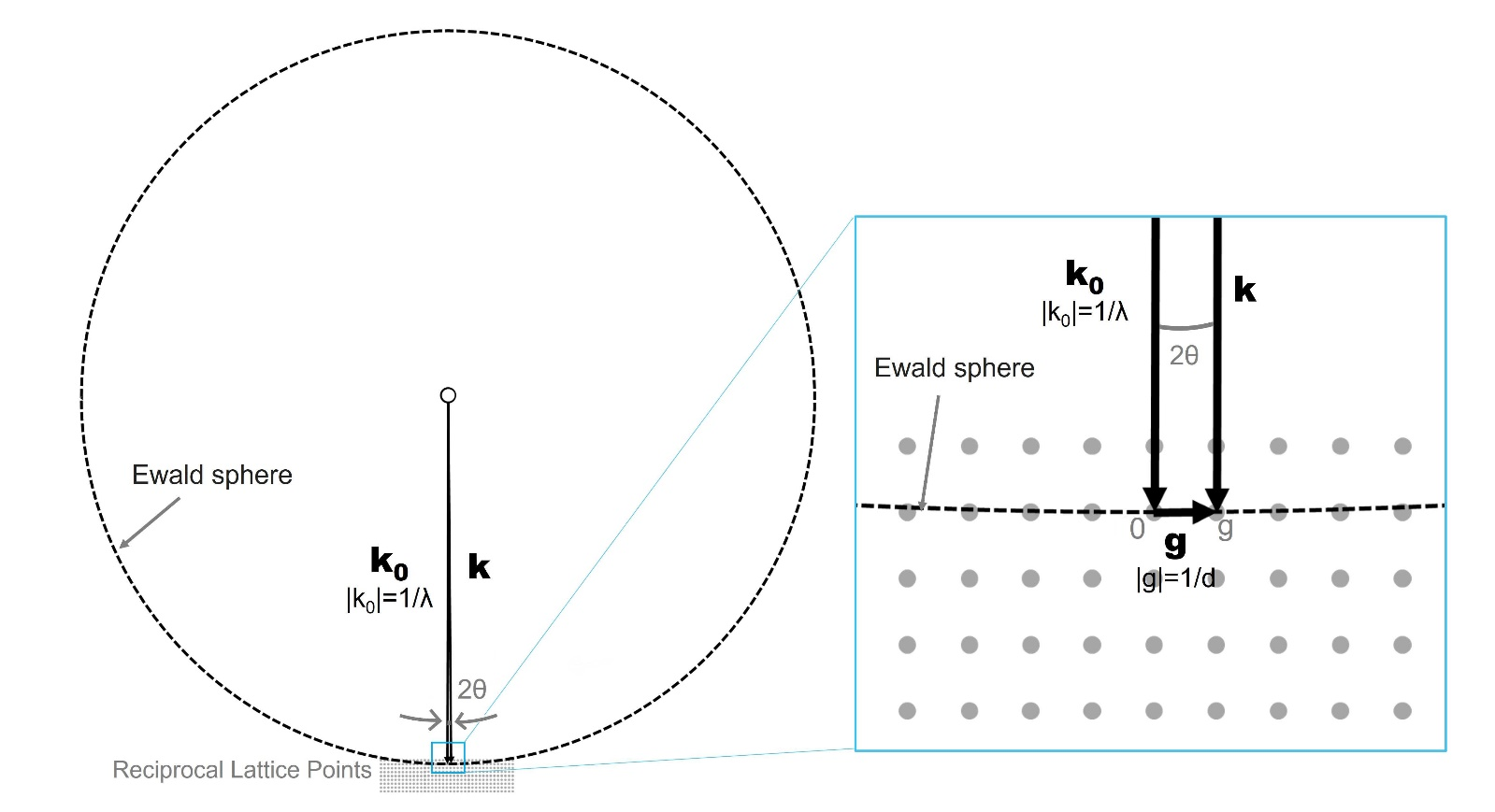
図：　逆格子とエワルド球。
左図では、原点付近での逆格子ベクトルgと入射ベクトルｋ₀、反射ベクトルｋの関係がわからないので、右図に拡大図を示した。
電子顕微鏡の場合は、加速電圧100kVの場合でもエワルド球の半径は27.0［Å^-1］になる。逆格子点の間隔は～0.5［Å^-1］なので、球の半径は逆格子点の間隔に比べて50倍以上になり非常に大きい。エワルド球は球というよりはほぼ平面に近くなっている。そのために、エワルド球は沢山の逆格子点とほぼ交わり、電子回折図形にはたくさんの反射が同時に現れる。

“Reciprocal lattice” is composed of the points (reciprocal lattice points) which are created in the directions perpendicular to the lattice planes at the distances reciprocal of the spacings of the (crystal) lattice planes in the real space. The reciprocal lattice is derived uniquely from the real lattice through a mathematical transformation.

The basis vectors a*, b* and c* of the reciprocal lattice are defined by the following equations using the basis vectors a, b and c of the real lattice.

Each denominator of these equations is equal to the volume V of the unit cell of the real lattice. That is,

V=a∙(b×c)=b∙(c×a)=c∙(a×b).(2)

Then, a*, b* and c* are written as

a* is vertical to the plane spanned by b and c of the real lattice. In the same manner, b* is vertical to the plane spanned by c and a, and c* is vertical to the plane spanned by a and b.

The reciprocal lattice is constructed by a linear combination of a*, b* and c*. The reciprocal lattice vector g is written with integers h,k,l as

g = ha*＋kb*＋lc*.(4)

The reciprocal lattice vector g is vertical to the crystal lattice plane (h k l) (termed “Miller index”) in the real space. The magnitude (length) of the vector g is reciprocal of the spacing d of the lattice plane (h k l), or｜g｜＝ 1/d. The dimensions of basis vectors of a*, b* and c* are [r]^-1, whereas the dimensions of basis vectors of a, b and c are [r]¹. So, the lattice constructed by a*, b* and c* is called “reciprocal lattice”.

The advantage of using the reciprocal lattice is that a crystal lattice plane can be treated as a reciprocal lattice point, that is “planes” are expressed as “points”. When the Ewald construction in the reciprocal lattice space is used, it is easy to find which lattice planes satisfy the reflection condition (Bragg condition). Drawing of the Ewald’s diagram is carried out in the following manner.

The dots in the figure show the reciprocal lattice points. Select one of the reciprocal lattice points and set the origin at a point that is 1/λ(=|k₀|) distant from that point in the direction anti-parallel to the direction of the incident electron beam. Draw an arrow line from the origin to the chosen reciprocal lattice point. The arrow line is the vector k₀ of the incident electron beam. Then, draw a sphere of radius 1/λ centered on the origin (Note that the figure shows not a sphere but a two-dimensional circle). This is called the Ewald sphere. All of the reciprocal lattice points intersecting the Ewald sphere satisfy the Bragg condition. A vector ｋ from the origin to a reciprocal lattice point g is the vector of the reflected beam. From the figure, the following equation is derived as the reflection condition.

ｋ-ｋ₀ = g.(5)

This is named the Laue condition. The incident beam withｋ₀ is reflected by a lattice plane (h k l) of a crystal and changes its direction by g toｋ=ｋ₀＋g, and is outgoing from the crystal in the directionｋ.

Letting the angle between ｋ₀ and ｋ be 2θ, the magnitude of ｋ-ｋ₀ becomes ( $\frac{1}{\lambda }$ )×2sinθ. Since the magnitude of g is 1/d, the following equation is obtained from eq.(5).

This equation is rewritten as

2dsinθ=λ.(7)

Equation (7) is the Bragg equation. Therefore, it becomes clear that the Laue condition derived from the Ewald’s diagram is equivalent to the Bragg condition.

The Bragg condition expresses diffraction by a crystal using a scalar quantity in the real space. Thus, the Bragg condition is intuitive and easy to understand. On the other hand, the Laue condition expresses diffraction using a vector quantity in the reciprocal space. Thus, the Laue condition is abstract but is suitable for theoretical treatment of diffraction phenomena. The use of the Laue condition is crucial for advanced theory of diffraction.

Fig. Reciprocal lattice and Ewald sphere. An enlarged figure of the bottom part in the left diagram is shown on the right to see the relation between the reciprocal lattice vector g and the incident wave vector k₀ & the reflection wave vector k.
In the case of the electron microscopy, the radius of the Ewald sphere is 27.0 [Å^-1] even at an acceleration voltage of 100 kV. The spacing of the reciprocal lattice points is ~0.5 [Å^-1]. Then, the radius of the sphere is very large, more than 50 times larger than the spacing of the reciprocal lattice points. The Ewald sphere is regarded approximately as a flat plane. Thus, the Ewald sphere nearly intersects many reciprocal lattice points and many reflections appear simultaneously in the electron diffraction pattern.

関連用語から探す