グリーン関数

Green's function

グリーン関数G(x,x') は、x’ にある点散乱体が点x に及ぼす影響（応答や伝搬）を与える関数である。以下では二つの数理モデルを例に挙げ、グリーン関数を用いた問題の解法を説明する。

例1。電荷分布ρが作るポテンシャルφの満たす方程式 Δφ=-ρ/ε₀ (Poisson方程式) を考える。もし、Ĝ=Δ^-1 であるような微分作用素の逆が得られれば、φ=-Ĝρ/ε₀ のようにして解が得られる。この積分作用素Ĝをグリーン演算子と呼び、実空間で表した積分核 G( x, x' ) ≔ ⟨ x│Ĝ│x' ⟩ をグリーン関数と言う。定義よりΔ⋅Ĝ=1 (恒等変換) となるので

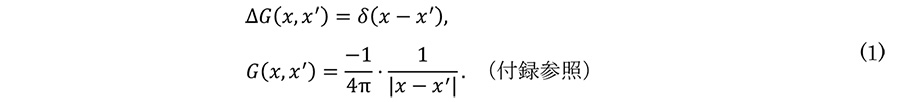
これを用いて、φの積分形式の解を得る。

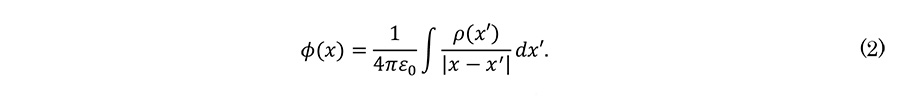
ここで、G(x,x')は点x’ にある電荷ρ(x') が点xに形成するポテンシャルφ(x)を与える応答関数ととらえることができる。

例2。電子線の動力学理論では、結晶に入射した電子は定常状態のシュレーディンガー方程式 [Δ+K²]ψ=-Uψ に従う。ここで、電子線の波数ベクトル K, 結晶のポテンシャルエネルギー分布 U(r) とする。Ĝ=[Δ+K² ]^-1 とおいて、ψ=-ĜUψ および、[Δ+K² ]⋅Ĝ=1 より、次の式が得られる。

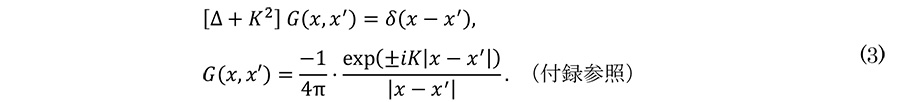
これを用いて、積分形式解を得る。

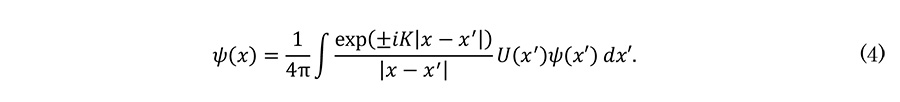
ここでは、G(x,x') は点x’ にある波動関数 ψ(x') と散乱体 U(x') が点x に形成する波動関数 ψ(x) を与える応答関数である。もしくは、散乱体 U によって電子波の状態が |x' ⟩ から|x ⟩ へ遷移する確率を与える伝搬関数ととらえることもできる。
等式 (4) は、求めるべきψが右辺の積分の中にも入っているので、逐次近似によって解を求める。散乱問題では無限遠点の解 (U =0の特殊解) を入射平面波φ(x' )=exp(iKx')とし、これを(4)式の右辺に代入した一次近似解を ψ=φ-ĜUφ のようにして求める（ボルン近似）。これは一回散乱した散乱波を求めることに相当し、振幅はUのフーリエ係数に比例する。

付録

【式(1)の証明】

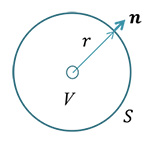
原点を中心とする半径 r の球をV、その表面をS とする。Gaussの発散定理により、

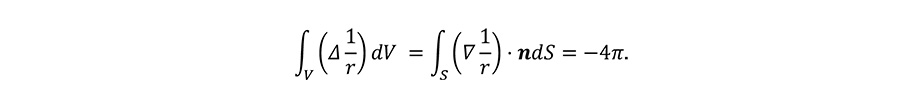
この積分は半径rによらないことから、被積分関数がδ関数であることがわかる。すなわち、

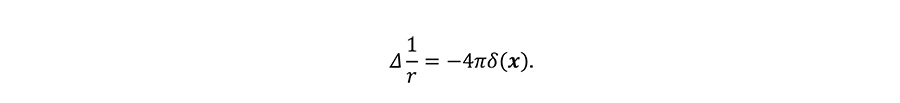
【式(3)の証明】

式(1)の類推から、式(3)の解は G(x,x')= f(r)/r, (r=|x-x'|) の関数形であると推測できる。これを代入して f''+K²f=0. したがって f(r)=C exp(±iKr) となり与式を得る。

The Green's function G(x,x') is a function that gives the effect (response and propagation) of a point scatterer at x' on a point x. In the following, two mathematical models are used as examples to explain how the Green's function is used to solve the problems.

Example 1. Consider the equation Δφ=-ρ/ε₀ (Poisson's equation), which is satisfied by the potential φ produced by the charge distribution ρ. If the inverse of the differential operator such that Ĝ=Δ^-1 is obtained, the solution can be obtained as φ=-Ĝρ/ε₀. The integral operator Ĝ is called the Green operator, and the integral kernel G( x, x' ) ≔ ⟨ x│Ĝ│x' ⟩ expressed in real space is called the Green's function.

From the definition, Δ⋅Ĝ=1 (Identity transformation), the following equations are derived.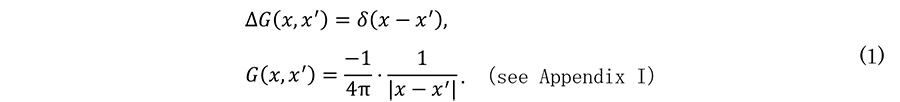

Then, the integral form solution of φ is obtained.

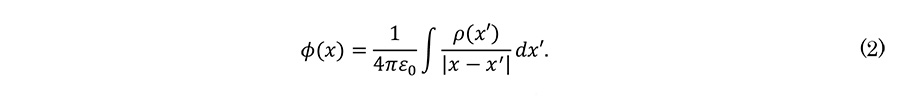
Here, G(x,x') can be regarded as a response function that gives the potential φ(x) formed at the point x by the charge ρ(x') at the point x’.

Example 2. In the dynamical theory of electron diffraction, an electron incident on a crystal follows the steady-state Schrodinger equation [Δ+K²]ψ=-Uψ, where K is the wave number vector of the incident electron and U(r) is the potential energy distribution of the crystal.
By letting Ĝ=[Δ+K² ]^-1, the solution can be obtained as ψ=-ĜUψ. From the definition, [Δ+K² ]⋅Ĝ=1 (Identity transformation), the following equations are derived.

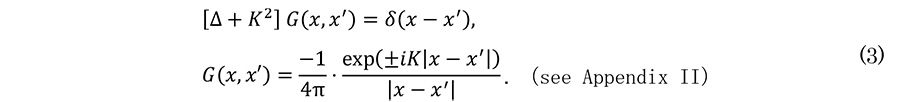
Then, the integral form solution of ψ is obtained.

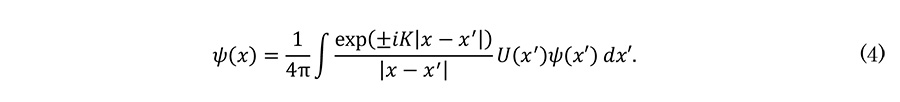
Here, G(x,x') can be regarded as a response function that gives the wave function ψ(x) formed at the point x by the wave function ψ(x') and the scatterer U(x') at the point x'. It can also be regarded as a propagator that gives the probability of the change of the electron wave from |x' ⟩ to that of |x ⟩ by the scatterer U.

Equation (4) is solved by an iterative approximation, since ψ is also included in the integral on the right-hand side.
In the scattering problem, the solution at infinity (particular solution for U=0) is the incident plane wave φ(x')=exp(iKx'). The first-order approximate solution is obtained by substituting the plane wave into the right-hand side of eq. (4) as ψ=φ-ĜUφ (Born approximation). This formulation corresponds to finding the scattered wave that is scattered only once, and the resulting scattering amplitude is proportional to the Fourier coefficient of U.

Appendix I. Proof of eq. (1).

Let V be a sphere with radius r centered on the origin, and S be its surface. Then, from Gauss's divergence theorem we obtain,

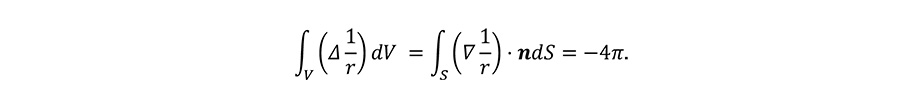
Since the integral does not depend on the radius r, the integrand is proved to be a delta function, i.e.,

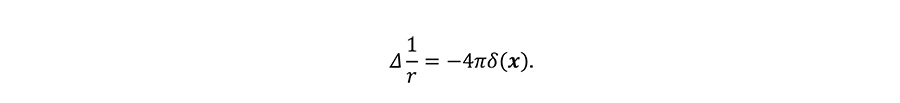
Appendix II. Proof of eq. (3).

From the analogy of eq. (1), the solution of eq. (3) is expected in a form of G(x,x')= f(r)/r, (r=|x-x'|). Substituting this, we obtain f''+K²f=0. By solving this equation, we obtain f(r)=C exp(±iKr).