散乱断面積

scattering cross section

[目次：理論(電子の散乱／回折／結像)]

入射電子が原子によって散乱される確率を面積の単位で表わしたもの。
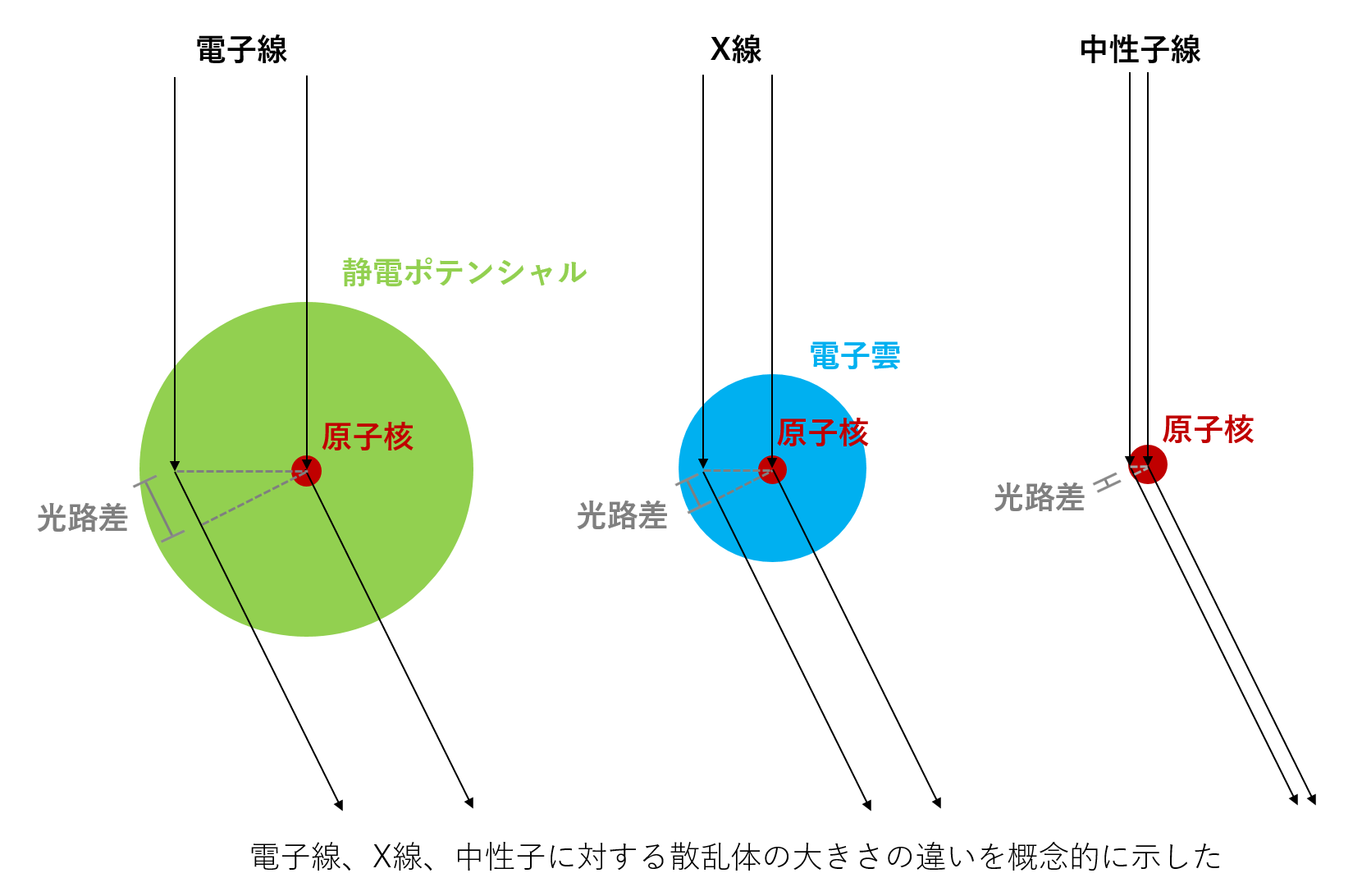
入射電子に対する原子散乱因子（原子形状因子）と散乱断面積の関係は以下の通りである。原子散乱因子（単位は［V］［ų］）に2πme/h²=2.09x10^-2（［V^－1］［Å^¯2］）を掛けたものが散乱径（［Å］）であり、それを二乗したものが散乱断面積（［Ų］）になっている。原子は有限の大きさを持つので、低角度散乱では原子の内側と外側で散乱される電子の位相のずれが小さく、散乱断面積は大きい。高角度散乱になるにしたがって原子の内側と外側で散乱電子の位相差が大きくなり、干渉性が悪くなるので、散乱断面積は小さくなる。
なお2πme/h²は、シュレーディンガー方程式で散乱問題を解くときに出てくる係数である。
ここで、mは電子の質量、eは電子の電荷、hはプランク定数である。

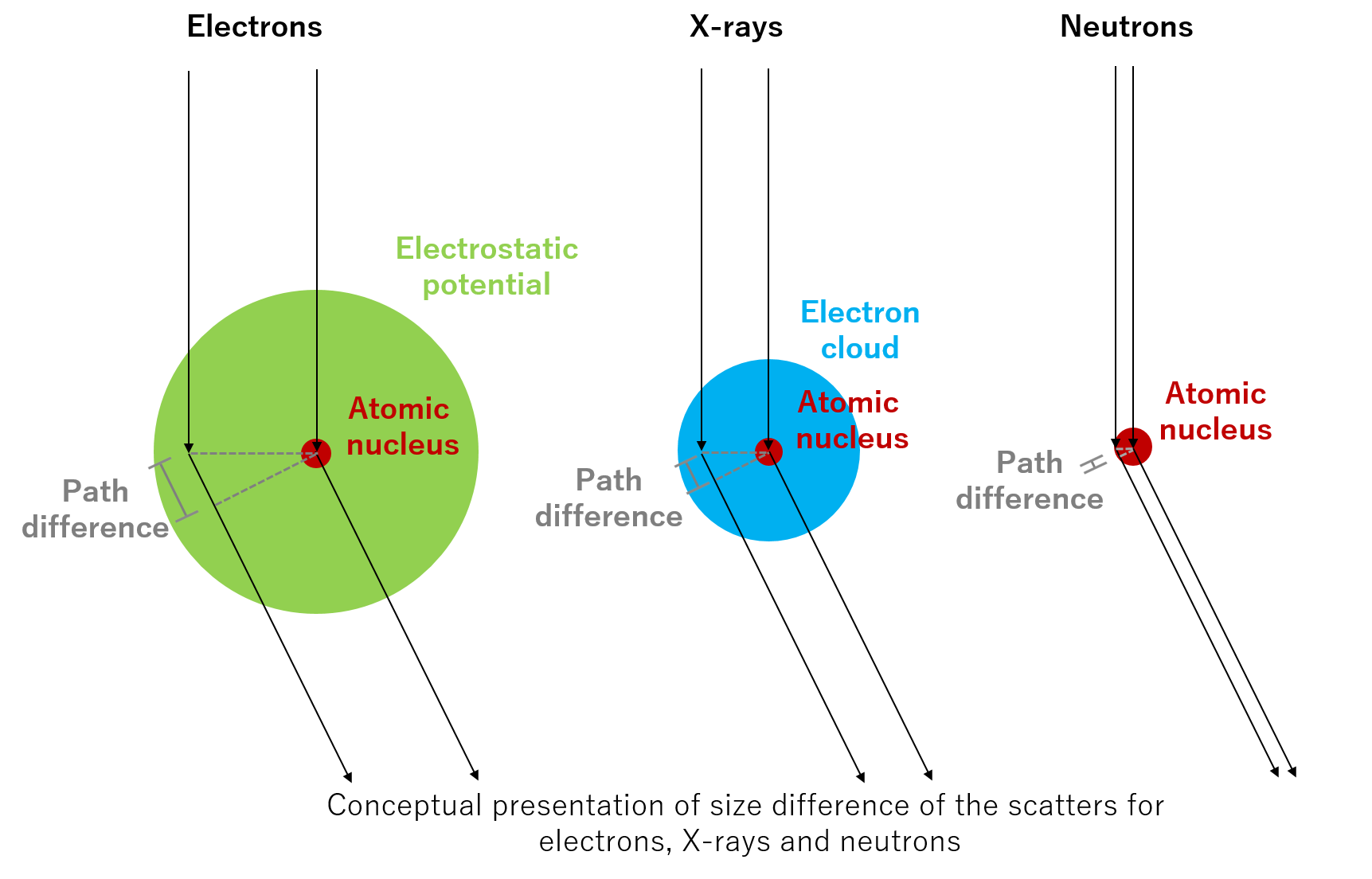
The scattering cross section is the scattering probability of an incident electron being scattered by an atom, expressed by the unit of area.
The relation between the atomic scattering factor (atomic form factor) and the scattering cross section for incident electrons is as follows.
The atomic scattering factor for an incident electron (in units of [V][ų]) multiplied by 2πme/h²=2.09x10^-2 ([V^¯1][Å^¯2]) is the scattering length ([Å]). The square of the scattering length is the scattering cross section ([Ų]).
Since the atom size is finite, the scattering cross section is large at low scattering angles because the phase difference between the electrons scattered by the inner part and outer part of the atom is small. As scattering angles become large, the cross section becomes small because the phase difference between those electrons becomes large, and thus the interference of those electron waves is destructive.
It is noted that 2πme/h² is the coefficient that appears when solving scattering problem using the Schrödinger equation. Here, m is the mass of an electron, e is the charge of an electron, and h is Planck’s constant.

関連用語から探す