デルタフリンジ

δ fringe

[目次：理論(電子の散乱／回折／結像)]

結晶性薄膜試料の表面に対して斜めに入る双晶境界（もっと一般に、結晶方位の違いがある界面）を二波近似回折条件で撮影するとき、明視野像および暗視野像に現れる特定のコントラストを持つ縞のこと。

図1に、試料の表面に対して斜めに入る双晶境界からの縞状のコントラストとその模式図を示す。図1(a)は、双晶境界とそれによって作られる縞状のコントラストを模式的に示す。結晶の格子面は双晶境界の両側で方位が変わる（角度が変わる）。図1(b)は、酸化ニッケル (NiO)の試料の表面に対して斜めに入る双晶境界からの暗視野像である。図1(c)は、図1(b) の拡大図である。両側の結晶では回折波ｇの励起誤差ｓが異なる。両結晶での励起誤差ｓの差 Δｓ＝ｓ₁−ｓ₂ の正負によって両端の縞のコントラストの特徴が決まる。縞のコントラストは吸収効果を取り入れた動力学理論によって説明される。

双晶境界が試料の上下の表面と交わるところに現れる縞のコントラストが、縞の中央（試料の厚さの半分の位置）に関して、暗視野では対称になるが、明視野では反対称になる。図1(b)および(c)で、両端の縞が中央に対して対称、すなわち白(B)と白(B)のペアになっているのが分かる。縞の対称性から、2つの結晶領域間の励起誤差の差 Δｓの正負(なす角の正負)や試料に対する界面の傾きの向き（右肩上がりか、左肩上がりか）が分かる。（図1(b)の場合はΔｓは正）詳細は文献 Marc De Graef : Introduction to Conventional Transmission Electron Microscopy, pp507~ を参照のこと。δフリンジの名称は双晶境界での結晶の方位変化 δ に由来する。

しかし、このような縞の対称性が現れるのは、二つの結晶領域のなす角度の差が数度以内のときである。それより角度が大きくなると、一方の領域しか回折条件を満たさなくなり（他方の励起誤差ｓが大きくなり）、δフリンジを特徴付ける縞の対称性は失われ、回折条件を満たした領域だけからの等厚干渉縞になる。したがって、δフリンジは、αフリンジとの対比において、また吸収効果を取り入れた動力学理論の検証としての意味はあるが、δフリンジから結晶領域間の角度の測定はできない。

結晶領域間の方位の違い（なす角度）は、大角度収束電子回折法を用いて極めて高い精度で測定できる。以下の文献を参照すると良い。

• M. Tanaka, M. Terauchi and T. Kaneyama: J. Electron Microscopy 40 (1991) 211-220
• M. Tanaka, M. Terauchi and K. Tsuda: Convergent Beam Electron Diffraction III (1994) pp188-205, JEOL Tokyo

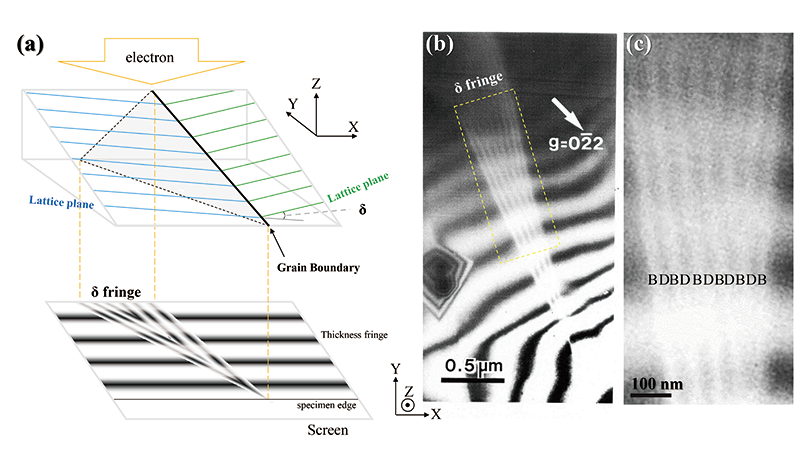
図1(a): くさび形の試料に斜めに入った結晶粒界(上)とδフリンジの模式図(下)。
図1(b): 試料の表面に対して斜めに入った双晶境界の暗視野像。両端の縞が白(B)と白(B)のペア（すなわち中央に対して対称）になっている。試料はチタン酸化ニッケル(NiO)。加速電圧200kV。
図1(c): (b)の黄色点線部の拡大図。両端の縞が白(B)と白(B)のペアが一層よく見える。

"δ fringe" means the edge fringes showing a specific contrast of the striped interference image obtained from a twin boundary oblique to a crystalline specimen surface, which appears in bright- and dark-field images taken at a two-wave approximation condition. (The twin boundary is formed by two crystalline parts with different orientations.)

Fig.1(a) shows a schematic of a twin boundary oblique to the specimen surface and the expected striped interference image or the δ fringe from the boundary. The lattice planes change their orientations at the twin boundary. Fig. 1(b) shows the dark-field image of a twin boundary of nickel oxide (NiO). Fig. 1(c) shows an enlarged image of a part of Fig. 1(b).
The excitation error s of diffracted wave g is different for the two crystalline regions of the twin. The sign of the difference Δs = s₁ - s₂ between the excitation errors s₁ and s₂ for the two regions, determines the nature of the end-striped image or the contrast of the δ fringe. The nature and formation of the striped image is explained by the dynamical diffraction theory taking account of the absorption effect. (see Reference: Marc De Graef: Introduction to Conventional Transmission Electron Microscopy, pp507~).
The end stripes or δ fringes, which appear at the intersection between the twin boundary and the upper and lower surfaces of the specimen, exhibit symmetric contrast in the dark-field image and anti-symmetric contrast in the bright-field image with respect to the center of the striped image (to the half depth position of the specimen). The symmetric contrast (nature) in the dark-field image or a bright (B)- and bright (B)-fringe pair is clearly seen in Fig. 1(b) and (c).
This symmetry nature reveals the sign of Δs (Δs is positive in Fig. 1(b)), and the sign of the angle between the two crystalline regions (the right region is upward to the left region or downward to the left). The term "δ fringe" is originated from the angular change "δ" between the crystalline regions at the twin boundary.
The symmetry nature above described appears only when the angular difference between the two crystalline regions is several degrees or less. If the angle becomes large, only one crystalline region satisfies the Bragg condition, that is, the excitation error s for the other region becomes large, the symmetry nature of the end stripes or the δ fringe disappears, and instead, equal thickness fringes appear from the former region where the diffraction condition is satisfied. Thus, understanding of the δ fringe together with the α fringe is one of the great successes of the dynamical diffraction theory taking account of the absorption effect. However, the angle between the two crystalline regions is difficult to be measured using the δ fringe.
It should be noted that the measurement of the angular difference between the two crystalline regions can be performed by the large-angle convergent-beam electron diffraction (LACBED) with a very high accuracy. The following references are referred to detailed LACBED analysis.

• M. Tanaka, M. Terauchi and T. Kaneyama: J. Electron Microscopy 40 (1991) 211-220
• M. Tanaka, M. Terauchi and K. Tsuda: Convergent Beam Electron Diffraction III (1994) pp188-205, JEOL Tokyo

Fig. 1(a) Schematic of a twin boundary oblique to a wedge-shaped specimen (top) and the illustration of the δ fringe (bottom).
Fig. 1(b) Dark-field image of a twin boundary oblique to the specimen surface, showing striped images and δ fringes. A bright (B)- and bright (B)-fringe pair is seen at the ends of the stripes (symmetric with respect to the center of the stripes). Specimen: NiO. Accelerating voltage: 200 kV.
Fig. 1(c) Enlarged image of (b) indicated by a yellow dotted line. The bright (B)- and bright (B)-fringe pair is more clearly seen at the both ends of the stripes.

関連用語から探す