フーリエ変換

Fourier transform

[目次：画像処理(画像処理／波形処理)]

ある関数をその変数に共役な変数の関数に変換する方法。例えば、時間の関数としての光や音のシグナルを周波数の関数として表したり(スペクトル分解)、位置の関数としての物体(結晶ポテンシャル)による散乱波を波数の関数としての回折図形 (結晶構造因子)に変換したりするときに使われる。

透過電子顕微鏡のレンズによる結像系は Fraunhofer回折として取り扱えるため、試料(結晶ポテンシャル)による散乱波→回折図形→像の一連の変換を、フーリエ変換と逆フーリエ変換の繰り返しと考えることができる。

ここで、ψ(r) は試料による散乱波で実空間 r の関数、 Ψ(k)はレンズにより後焦点面上に作られた回折波で、逆空間 k[1/m]の関数である。1番目の式は、試料による散乱波を回折図形に変換するフーリエ変換に対応し、2番目の式は、回折図形を試料の像に変換する逆フーリエ変換に対応する。

レンズによる結像（像と回折図形）⇒図1
透過電子顕微鏡の結像は、試料による散乱波→回折図形→像の一連の変換を試料のフーリエ変換と逆フーリエ変換を繰り返したものと考えることができる。ψ(r) は試料の散乱波で実空間上の関数、Ψ(k)はレンズにより後焦点面上に作られた回折波で逆空間上の関数である。Φ(x)∝ψ(x/M) は結像された散乱波で、レンズによる像の倍率 M および像の倒立を除いて ψ(r) に等しい。

(a) 金の結晶からの回折(フーリエ変換) 図形。(b) 結晶格子の像とそのFFTパターン。加速電圧：300kV、試料：金単結晶。⇒図2

結晶格子の周期性は、フーリエ変換によって、その周期と方向に対応する空間周波数の位置に明るい点(回折スポット)として現れる(a)。レンズの結像作用(逆フーリエ変換)によって、回折スポットから結晶格子の拡大した像が作られる (b)。

A method that transforms a function of certain variables into a function of the variables conjugate to the certain variables. For example, "Fourier transform" is used for light or sound as a function of time to express it as a function of frequency (spectral analysis), or for scattered waves from an object or a crystal potential as a function of position to transform it into a diffraction pattern or crystal structure factors as a function of wavenumber.

The imaging lens system of a TEM can be considered as a system in which scattered waves from an object or a crystal potential are Fourier transformed into a diffraction pattern and subsequently inverse Fourier transformed to an image of the object, where the assumption of Fraunhofer diffraction is applied.

Here, ψ(r) stands for the scattered waves from the specimen, being a function of the real space r, and Ψ(k) for the diffracted waves formed on the back focal plane of the imaging lens, being a function of the reciprocal space k [1/m]. The first equation expresses Fourier transform. That is, the scattered waves ψ(r) produced by the specimen are transformed to a diffraction pattern Ψ(k). The second equation expresses inverse Fourier transform. That is, the diffraction pattern Ψ(k) is transformed to a specimen’s image ψ(r).

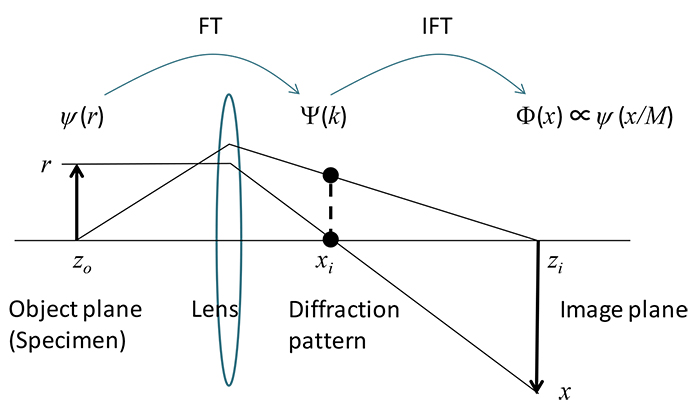
Fig. 1 TEM imaging by a lens (image and diffraction pattern)
The imaging process of a transmission electron microscope can be considered as a series of Fourier transform from scattered waves from a specimen to a diffraction pattern and of inverse Fourier transform of the diffraction pattern to an image of the specimen. ψ(r) expresses scattered waves of the specimen, being the function of position r, and Ψ(k) expresses diffracted waves formed on the back focal plane of the imaging lens, being a function of the wave number k [1/m]. Φ(x)∝ψ(x/M) expresses the scattered waves on the imaging plane, which is an image of the specimen, being the function of position r. It is noted that Φ(x) is equal to ψ(r) shown in the second equation, except for a magnification M and image inversion caused by the lens.

Fig. 2 (a) Diffraction pattern (Fourier transform pattern) of an Au crystal. (b) Crystal lattice image of the Au crystal and its FFT pattern. Accelerating voltage: 300 kV.

Periodicities of the crystal lattice appear as bright diffraction spots on the back focal plane of the lens depending on the spacing and orientation of the lattice, by Fourier transform (a). A magnified image of the crystal lattice is obtained from the diffraction spots by inverse Fourier transform (imaging process of the lens) (b).

関連用語から探す